Bonjour j'ai un exercice mais je n'arrive pas à le faire,si vous pouviez m'aider.Merci d'avance.
Un graphique dans un repère orthonormal,la branche d'hyperbole d'équation y=1/x avec x supérieur à 0.
A est le point de coordonnées (1;-1) et M de coordonnées (x;1/x).
Le but de l'exercice est de déterminer, s'il existe, le point M pour lequel la distance AM est minimale.
1.a) Justifiez que "AM est minimale" équivaut à "AM^2 est minimale".
b) Calculez en fonction de x, d(x)=AM^2
2. Démontrez que pour tout x supérieur à 0,d'(x)=(2f(x))/x^3 où f est un polynôme de degré 4.
3. Etude de f
a)Etudiez les variations de f sur I = ]0;+ l'infini[.
Démontrez que l'équation f(x)=0 admet une unique solution alpha dans I
Déterminer un encadrement de alpha d'amplitude 10^(-2).
c) Déduisez-en le signe de f sur I.
4. Déduisez de ce qui précède les variations de d et concluez.
5. Justifiez que si M est le point le plus proche de A alors (AM) est perpendiculaire à la tangente en M à l'hyperbole.
Optimisation
4 messages
- Page 1 sur 1
Bonjour,
1.a Il suffit de dire que les distances sont des nombres positifs, et que comparer deux nombres positifs revient à comparer leurs carrés (dans le même sens)
1.b Il te suffit d'utliliser la formule qui donne la distance entre deux points A et B :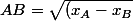^2 + (y_A - y_B)^2}) et de l'appliquer à ton point A et à ton point M pour calculer la distance AM.
et de l'appliquer à ton point A et à ton point M pour calculer la distance AM.
Je m'arrête là pour l'instant, et te laisse chercher la suite. Tu n'as pas indiqué où tu bloquais, donc je suppose que tu bloquais dès le début. La prochaine fois, indique où tu en es et sur quoi tu bloques.
Redemandes si tu n'arrives pas à faire la suite (en indiquant bien à quelle question tu en es).
1.a Il suffit de dire que les distances sont des nombres positifs, et que comparer deux nombres positifs revient à comparer leurs carrés (dans le même sens)
1.b Il te suffit d'utliliser la formule qui donne la distance entre deux points A et B :
Je m'arrête là pour l'instant, et te laisse chercher la suite. Tu n'as pas indiqué où tu bloquais, donc je suppose que tu bloquais dès le début. La prochaine fois, indique où tu en es et sur quoi tu bloques.
Redemandes si tu n'arrives pas à faire la suite (en indiquant bien à quelle question tu en es).
oui exact j'ai oublié de dire où je bloquais.
j'ai déjà calculé AM= [(1-x)^2+(-1-(1/x)^2]
[(1-x)^2+(-1-(1/x)^2]
dérivée de (AM^2)'=-2*(1-x) + (2/x^2)*(-1-(1/x))
= (2x^4 - 2x^3 - 2x -2)/(x^3)
donc f(x)=x^4-x^3-x-1
alors f '(x)=4*(x)^3 - 3*(x^2) - 1
=(x-1)*(4*(x^2)+x+1)
Je ne sais pas si c'est bon ce que j'ai fais jusqu'ici mais,je bloque pour étudier les variations de I=]o;+l'infini[ car dans les racines je trouve pour x-1=0 , x=0 et pour le trinome il n'y a pas de racines car delta est inférieur à 0.Mais dans le tableau de variation je trouve que f est croissante sur ]1;+l'infini[.je ne pense pas que ce soit le résultat attendu,j'ai surement du faire une erreur avant mais je ne vois pas...
j'ai déjà calculé AM=
dérivée de (AM^2)'=-2*(1-x) + (2/x^2)*(-1-(1/x))
= (2x^4 - 2x^3 - 2x -2)/(x^3)
donc f(x)=x^4-x^3-x-1
alors f '(x)=4*(x)^3 - 3*(x^2) - 1
=(x-1)*(4*(x^2)+x+1)
Je ne sais pas si c'est bon ce que j'ai fais jusqu'ici mais,je bloque pour étudier les variations de I=]o;+l'infini[ car dans les racines je trouve pour x-1=0 , x=0 et pour le trinome il n'y a pas de racines car delta est inférieur à 0.Mais dans le tableau de variation je trouve que f est croissante sur ]1;+l'infini[.je ne pense pas que ce soit le résultat attendu,j'ai surement du faire une erreur avant mais je ne vois pas...
optimisation
j'ai réussi tout l'exercice sauf le 5.; je crois qu'il faut faire avec le produit scalaire mais je n'y arrive pas.si quelqu'un peut m'aider svp.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
