Optimisation de distance
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 01 Sep 2016, 11:49
par beagle » 01 Sep 2016, 11:49
Grizet a écrit:L'angle formé par les 2 segments du trajet est bien de 90° ? Si oui, peut on prouver que cet angle est l'angle pour optimiser la distance du trajet ?
non pas du tout
Pour t'en convaincre place deux points à même distance de la droite
met les deux symétriques par rapport à la droite
ben cela construit un rectangle, et les diagos du rectangle ne se croisent pas à angle droit (sauf si carré, prend un bon rectangle allongé pour t'en convaincre)
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 02 Sep 2016, 00:27
par Razes » 02 Sep 2016, 00:27
Soit

et

les deux points et soit
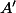
et
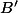
leurs projections sur la droite
)
. Soi

le point recherché de
)
. Le trajet optimisé impose que le point

doit se trouver ente
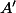
et
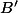
.
On pose

et
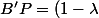A'B')
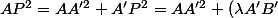^2)
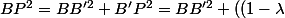A'B')^2)
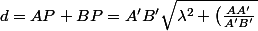^2}+A'B'\sqrt{(1-\lambda)^2+\left ( \frac{BB'}{A'B'} \right )^2}=A'B'f(\lambda ))
Le minimum de la distance correspond au minimum de
)
Calculons
)
, la condition de minimum correspond donc à
=0)
.
Faites les calculs, on aboutis à l'expression
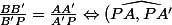=(\widehat{PB, PB'}))
Les deux angles sont égaux. Ce qui correspond à la réflexion en optique et la solution proposée initialement.
Modifié en dernier par
Razes le 02 Sep 2016, 08:21, modifié 1 fois.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 02 Sep 2016, 08:06
par beagle » 02 Sep 2016, 08:06
Pythagore ou Thalès.
Idem on garde A' et B' projections sur (D), on met en plus B" symétrique de B par rapport (D),
donc l'idée de Chan79:
AP + PB = AP +PB"
or min de AP+PB" quand APB" alignés.
Thalès AA'/ B'B" = A'P/PB'
et B'B" = BB'
donc P entre AA' dans le même rapport que les rapports de distances des points A et B à la droite.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 02 Sep 2016, 08:21
par beagle » 02 Sep 2016, 08:21
Donc comment avoir l'idée de Chan79?
La pratique déjà,
ensuite c'est assez classique de rajouter des points pour voir si ce n'est pas plus facile,
si les équivalences de longueur n'arrivent pas plus facilement juste à coté
avec cet adage:
"Quand le prof de maths montre le segment PB l'idiot regarde PB.
ici fallait tourner la tète vers PB"
alors des points faciles à poser ce sont les symétriques.
Et idem la géométrie de collège c'est Pythagore ou Thalès,
donc tu cherches du Thalès dans l'exo, et là où tu ne le trouves pas directement, ben tu l'inventes à coté ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
Grizet
- Membre Naturel
- Messages: 95
- Enregistré le: 31 Juil 2016, 08:37
-
 par Grizet » 02 Sep 2016, 08:59
par Grizet » 02 Sep 2016, 08:59
C'est très complet et exactement ce que je cherchais, merci à tous ! Vous êtes formidables !
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 02 Sep 2016, 09:03
par Razes » 02 Sep 2016, 09:03
Bonne continuation.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 02 Sep 2016, 10:22
par Pseuda » 02 Sep 2016, 10:22
Razes a écrit:Soit

et

les deux points et soit
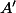
et
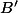
leurs projections sur la droite
)
. Soi

le point recherché de
)
. Le trajet optimisé impose que le point

doit se trouver ente
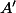
et
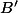
.
On pose

et
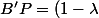A'B')
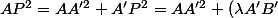^2)
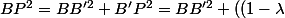A'B')^2)
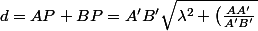^2}+A'B'\sqrt{(1-\lambda)^2+\left ( \frac{BB'}{A'B'} \right )^2}=A'B'f(\lambda ))
Le minimum de la distance correspond au minimum de
)
Calculons
)
, la condition de minimum correspond donc à
=0)
.
Faites les calculs, on aboutis à l'expression
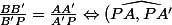=(\widehat{PB, PB'}))
Les deux angles sont égaux. Ce qui correspond à la réflexion en optique et la solution proposée initialement.
Bonjour,
Ouh là là ! Pourquoi faire si compliqué alors que c'est si simple ?
En appelant B' le symétrique de B par rapport à (D), et P le point d'intersection de (AB') avec (D) :

Donc le trajet qui passe par P est le plus court, et voilà.

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 02 Sep 2016, 14:03
par Razes » 02 Sep 2016, 14:03
@Pseuda Bonjour,
Ouh là là ! Pourquoi faire si compliqué alors que c'est si simple ?
En appelant B' le symétrique de B par rapport à (D), et P le point d'intersection de (AB') avec (D) :

Donc le trajet qui passe par P est le plus court, et voilà.

Merci de me rappeler ce que j'avais écris le
31 Aoû 2016 16:38 ;

La solution du
01 Sep 2016 23:27 est pour ceux qui aiment les formules mathématiques et les calculs et qui croient qu'il existent d'autres solutions.

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 02 Sep 2016, 18:33
par Pseuda » 02 Sep 2016, 18:33
Bonsoir,
Désolée, mais je ne vois pas vraiment l'intérêt de faire compliqué quand on peut faire simple. A mon sens (mais ce n'est peut-être pas le tien), cela n'a aucun intérêt mathématique. Et à mon sens toujours, les démonstrations les plus élégantes, et les plus convaincantes surtout, sont celles qui sont les plus simples.

Tu commences par dire que :
Razes a écrit: Le trajet optimisé impose que le point P doit se trouver ente A' et B'.
Qu'est-ce qui te permet de l'affirmer ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Sep 2016, 18:47
par zygomatique » 02 Sep 2016, 18:47
salut
juste pour info : l'inégalité triangulaire est à la base de cet exercice ... (et ça répond à la dernière question de pseuda)


l'idée du symétrique est un classique ... quand on fait de la géométrie (élémentaire) utilisant les transformations de base : réflexion, translation, symétrie centrale et rotation
...
évidemment dans le plan euclidien le plus court chemin entre deux points est la ligne droite ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 02 Sep 2016, 20:42
par Pseuda » 02 Sep 2016, 20:42
zygomatique a écrit:salut
juste pour info : l'inégalité triangulaire est à la base de cet exercice ... (et ça répond à la dernière question de pseuda)


l'idée du symétrique est un classique ... quand on fait de la géométrie (élémentaire) utilisant les transformations de base : réflexion, translation, symétrie centrale et rotation
...
évidemment dans le plan euclidien le plus court chemin entre deux points est la ligne droite ....
Je ne vois pas toujours pas en quoi cela explique l'affirmation de Razes au début de sa démonstration : " le trajet optimisé impose que le point P doit se trouver ente A' et B' (projetés orthogonaux de A et B sur la droite (D)). ". Enfin bref.
Sinon, d'accord avec : " l'inégalité triangulaire est à la base de cet exercice ".
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités


