Nombres complexes et lieux géométrique ,la différence entre le lexique
31 messages
- Page 1 sur 2 - 1, 2
nombres complexes et lieux géométrique ,la différence entre le lexique
Expliquer moi la différence entre le lexique utilisé dans les phrases suivantes
z' soit imaginaire pur;
z' soit imaginaire pur non nul;
z' soit imaginaire
Application
Soient A , B et M les points d'affixes respectives i,2i et z. Pour tout z (différent) i, on considère
z'=z-2i/(z+i) et le point M' d'affixe z'.
Déterminer les ensembles suivants en utilisant les arguments :
1) E, ensemble des points M tels que z' soit réel;
2) F, ensemble des points M tels que z' soit réel non nul;
3)G, ensemble des points M tels que z' soit imaginaire pur;
4) H, ensemble des points M tels que z' soit imaginaire pur non nul;
5) K , ensemble des points M tels que z' soit imaginaire
merci
z' soit imaginaire pur;
z' soit imaginaire pur non nul;
z' soit imaginaire
Application
Soient A , B et M les points d'affixes respectives i,2i et z. Pour tout z (différent) i, on considère
z'=z-2i/(z+i) et le point M' d'affixe z'.
Déterminer les ensembles suivants en utilisant les arguments :
1) E, ensemble des points M tels que z' soit réel;
2) F, ensemble des points M tels que z' soit réel non nul;
3)G, ensemble des points M tels que z' soit imaginaire pur;
4) H, ensemble des points M tels que z' soit imaginaire pur non nul;
5) K , ensemble des points M tels que z' soit imaginaire
merci
Salut !
Supposons que s'écrit sous la forme
s'écrit sous la forme 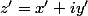 où
où  est la partie réelle de
est la partie réelle de  et
et  la partie imaginaire de
la partie imaginaire de  .
.
- est imaginaire pur signifie que
est imaginaire pur signifie que  ;
;
- est imaginaire pur non nul signifie que
est imaginaire pur non nul signifie que  et
et  .
.
- Par contre, j'ai du mal à voir quelle distinction on peut faire entre "imaginaire" et "imaginaire pur" : pour moi ils sont synonymes...
Qu'as-tu fait pour le moment ?
Où bloques-tu ?
Supposons que
-
-
- Par contre, j'ai du mal à voir quelle distinction on peut faire entre "imaginaire" et "imaginaire pur" : pour moi ils sont synonymes...
Qu'as-tu fait pour le moment ?
Où bloques-tu ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
comment utiliser les arguments
salut capitaine nuggets
merci pour les explications
j aime bien savoir comment utiliser les arguments avec modulo (2pi) pour répondre aux questions
c est ça mon problème
merci
merci pour les explications
j aime bien savoir comment utiliser les arguments avec modulo (2pi) pour répondre aux questions
c est ça mon problème
merci
rectification
salut zygomatique
pardonner moi
c est (z-2i)/(z+i)
comment utiliser les arguments modulo 2pi pour répondre aux questions
merci
pardonner moi
c est (z-2i)/(z+i)
comment utiliser les arguments modulo 2pi pour répondre aux questions
merci
Un point 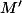 du plan complexe d'affixe
du plan complexe d'affixe  , peut également être vu comme l'affixe du vecteur
, peut également être vu comme l'affixe du vecteur 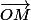 où
où ) est l'origine du repère orthonormé
est l'origine du repère orthonormé ) .
.
Ainsi, est réel si et seulement si
est réel si et seulement si 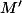 appartient à l'axe des abscisses.
appartient à l'axe des abscisses.
Or si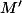 appartient à l'axe des abscisses, c'est que
appartient à l'axe des abscisses, c'est que =(\vec{u},\vec{OM'}) =0) [mod
[mod  ] ;
] ;
De même, est imaginaire pur si et seulement si
est imaginaire pur si et seulement si 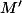 appartient à l'axe des ordonnées. Or si
appartient à l'axe des ordonnées. Or si 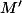 appartient à l'axe des ordonnées, c'est que l'on a
appartient à l'axe des ordonnées, c'est que l'on a =(\vec{u},\vec{OM'}) = \frac{\pi}{2}) [mod
[mod  ].
].
(Tout ça se voit bien sur un dessin).
Ici tu as , donc pose
, donc pose 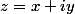 , aveec
, aveec  réels puis écrit
réels puis écrit  sous la forme
sous la forme  où
où 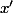 et
et 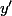 sont deux réels qui seront à exprimer en fonction de
sont deux réels qui seront à exprimer en fonction de  et
et  à priori.
à priori.
:+++:
Ainsi,
Or si
De même,
(Tout ça se voit bien sur un dessin).
Ici tu as
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
modulo 2pi
salut capitaine nuggets
merci pour ta réponse
une remarque
en ecrit autrement car on travaille avec modulo 2pi
(vect(u),vectOM')=(VectAM,vect BM)=0 mod 2pi ou (vect(u),vectOM')=(VectAM,vect BM)=pi mod 2pi
de même
(vect(u),vectOM')=(VectAM,vect BM)=pi/2 mod 2pi ou
(vect(u),vectOM')=(VectAM,vect BM)=-pi/2 mod 2pi
mes ensembles est que c es la droite (AB)- A,B ou (AB)- A comment le justifier
pour l autre cas cercle privé des points A et B ou cercle privé du point A seulement
mon problème c est a ce niveau
merci
merci pour ta réponse
une remarque
en ecrit autrement car on travaille avec modulo 2pi
(vect(u),vectOM')=(VectAM,vect BM)=0 mod 2pi ou (vect(u),vectOM')=(VectAM,vect BM)=pi mod 2pi
de même
(vect(u),vectOM')=(VectAM,vect BM)=pi/2 mod 2pi ou
(vect(u),vectOM')=(VectAM,vect BM)=-pi/2 mod 2pi
mes ensembles est que c es la droite (AB)- A,B ou (AB)- A comment le justifier
pour l autre cas cercle privé des points A et B ou cercle privé du point A seulement
mon problème c est a ce niveau
merci
georgets555 a écrit:salut capitaine nuggets
merci pour ta réponse
une remarque
en ecrit autrement car on travaille avec modulo 2pi
(vect(u),vectOM')=(VectAM,vect BM)=0 mod 2pi ou (vect(u),vectOM')=(VectAM,vect BM)=pi mod 2pi
de même
(vect(u),vectOM')=(VectAM,vect BM)=pi/2 mod 2pi ou
(vect(u),vectOM')=(VectAM,vect BM)=-pi/2 mod 2pi
merci
Oui
georgets555 a écrit:mes ensembles est que c es la droite (AB)- A,B ou (AB)- A comment le justifier
pour l autre cas cercle privé des points A et B ou cercle privé du point A seulement
mon problème c est a ce niveau
merci
Commence déjà par faire ce que j'ai dit lors de mon précédent message : tu exprimes
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Je viens de le faire et voici ce que te conseille : par la méthode que je t'ai donnée, montre que z' peut s'écrire sous la forme :
[CENTER]^2}+i \frac{-x}{x^2+(y+1)^2}) [/CENTER]
[/CENTER]
- est réel si et seulement si
est réel si et seulement si ^2}=0) ;
;
- est imaginaire pur
est imaginaire pur ^2}=0) (pour conclure ici, tu devras montrer que
(pour conclure ici, tu devras montrer que ^2-\frac 9 4) ).
).
Je te laisse poursuivre :lol3:
[CENTER]
-
-
Je te laisse poursuivre :lol3:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
salut capitaine nuggets
mon problème c est comment utiliser les arguments pour déterminer un ensemble de point sans utiliser la méthode analytique
svp si possible de me vérifier les remarques suivantes
- "imaginaire" et "imaginaire pur" : ils sont synonymes ?
au niveaux de leurs écriture en argument si possible de m expliquer leurs différences et donner les ensembles qu ils forment
1er cas z' est imaginaire pur
z'=0 ou ( z' est différent de 0 et argz'=pi/2 mod 2pi ou argz'=-pi/2 mod 2pi)
2em cas z' est imaginaire pur et non nul
argz'=pi/2 mod 2pi ou argz'=-pi/2 mod 2pi)
ici mon problème
z' imaginaire
3em cas z'=0 ou ( argz'=pi/2 mod 2pi ou argz'=-pi/2 mod 2pi)
merci
mon problème c est comment utiliser les arguments pour déterminer un ensemble de point sans utiliser la méthode analytique
svp si possible de me vérifier les remarques suivantes
- "imaginaire" et "imaginaire pur" : ils sont synonymes ?
au niveaux de leurs écriture en argument si possible de m expliquer leurs différences et donner les ensembles qu ils forment
1er cas z' est imaginaire pur
z'=0 ou ( z' est différent de 0 et argz'=pi/2 mod 2pi ou argz'=-pi/2 mod 2pi)
2em cas z' est imaginaire pur et non nul
argz'=pi/2 mod 2pi ou argz'=-pi/2 mod 2pi)
ici mon problème
z' imaginaire
3em cas z'=0 ou ( argz'=pi/2 mod 2pi ou argz'=-pi/2 mod 2pi)
merci
Ok, je vois deux autres manières (je raisonne juste sur le cas réel, le cas imaginaire étant analogue à priori) :
1) Comme il a été dit précédemment, est réel si et seulement si
est réel si et seulement si =0) ou
ou  [mod
[mod  ].
].  = \arg(z-2i) - \arg(z+i)) donc
donc  est réel si et seulement si
est réel si et seulement si  - \arg(z+i)=0) ou
ou  [mod
[mod  ].
].
- - \arg(z+i)=0) [mod
[mod  ] signifie que les vecteurs
] signifie que les vecteurs 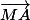 et
et 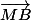 sont colinéaires et de même sens (c'est donc la droite
sont colinéaires et de même sens (c'est donc la droite ) privée de
privée de  ) ;
) ;
- - \arg(z+i)=\pi) [mod
[mod  ] signifie que les vecteurs
] signifie que les vecteurs 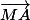 et
et 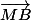 sont colinéaires de sens contraire (c'est donc
sont colinéaires de sens contraire (c'est donc  ).
).
2) est réel si et seulement si il existe un réel
est réel si et seulement si il existe un réel  tel que
tel que  , ou encore
, ou encore ) , ce qui revient à dire que les vecteurs
, ce qui revient à dire que les vecteurs 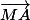 et
et 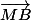 sont colinéaires sans pour autant oublier que
sont colinéaires sans pour autant oublier que 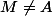 .
.
Donc en conclusion, est réel si et seulement si
est réel si et seulement si \setminus\{A\}) .
.
:+++:
1) Comme il a été dit précédemment,
-
-
2)
Donc en conclusion,
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
les points limites
salut capitaine nuggets
si possible de me traiter le cas imaginaire
juste une remarque
z' est réel si et seulement si \arg\left\( \frac{z-2i}{z+i} \right\)=0 ou \pi [mod 2\pi].
est ce qu il l ecrire autrement et ajouter
z' est réel si et seulement si z'=o ou z'différent de 0 et \arg\left\( \frac{z-2i}{z+i} \right\)=0 ou \pi [mod 2\pi]
2) \vec{MA} et \vec{MB} sont colinéaires et de même sens (c'est donc la droite (AB) privée de [AB[)
pourquoi le segment est privé du B et ne pas prendre [AB]
de même pour l autre cas c est prendre le segment ouvert
merci
si possible de me traiter le cas imaginaire
juste une remarque
z' est réel si et seulement si \arg\left\( \frac{z-2i}{z+i} \right\)=0 ou \pi [mod 2\pi].
est ce qu il l ecrire autrement et ajouter
z' est réel si et seulement si z'=o ou z'différent de 0 et \arg\left\( \frac{z-2i}{z+i} \right\)=0 ou \pi [mod 2\pi]
2) \vec{MA} et \vec{MB} sont colinéaires et de même sens (c'est donc la droite (AB) privée de [AB[)
pourquoi le segment est privé du B et ne pas prendre [AB]
de même pour l autre cas c est prendre le segment ouvert
merci
georgets555 a écrit:salut capitaine nuggets
si possible de me traiter le cas imaginaire
juste une remarque
z' est réel si et seulement si \arg\left\( \frac{z-2i}{z+i} \right\)=0 ou \pi [mod 2\pi].
est ce qu il l ecrire autrement et ajouter
z' est réel si et seulement si z'=o ou z'différent de 0 et \arg\left\( \frac{z-2i}{z+i} \right\)=0 ou \pi [mod 2\pi]
2) \vec{MA} et \vec{MB} sont colinéaires et de même sens (c'est donc la droite (AB) privée de [AB[)
pourquoi le segment est privé du B et ne pas prendre [AB]
de même pour l autre cas c est prendre le segment ouvert
merci
J'ai du mal à te relire...
En ce qui concerne 2), en fait il ne faut pas voir ça comme le segment
Tu peux également le voir comme ça : à la fonction
En gros,
Il faut bien comprendre la nature de ce que l'on recherche : un ensemble de point du plan
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
explication de la méthode
salut capitaine nuggets
merci pour les explications
si possible de m expliquer avec plus de détails ta remarque
(( Il faut bien comprendre la nature de ce que l'on recherche : un ensemble de point du plan \mathbb{P}, ou un ensemble d'affixe dans \mathbb{C}))
svp
au niveau de l écriture de l équivalence est ce que c est juste de l écrire de cette façon et ou est la faute
z' est rée si et seulement si z'=0 ou z'est différent de 0 ou argz'= o ou pi mod 2pi
est possible de me traiter le cas de z' imaginaire pur ou imaginaire avec les arguments
merci
merci pour les explications
si possible de m expliquer avec plus de détails ta remarque
(( Il faut bien comprendre la nature de ce que l'on recherche : un ensemble de point du plan \mathbb{P}, ou un ensemble d'affixe dans \mathbb{C}))
svp
au niveau de l écriture de l équivalence est ce que c est juste de l écrire de cette façon et ou est la faute
z' est rée si et seulement si z'=0 ou z'est différent de 0 ou argz'= o ou pi mod 2pi
est possible de me traiter le cas de z' imaginaire pur ou imaginaire avec les arguments
merci
georgets555 a écrit:si possible de m expliquer avec plus de détails ta remarque
(( Il faut bien comprendre la nature de ce que l'on recherche : un ensemble de point du plan \mathbb{P}, ou un ensemble d'affixe dans \mathbb{C}))
georgets555 a écrit:1) E, ensemble des points M tels que z' soit réel;
On te demande de chercher
Un exemple de ce que je veux dire (avec les mêmes données de l'énoncé) :
- Si on te demande de déterminer l'ensemble
- Si on te demande de déterminer l'ensemble
georgets555 a écrit:svp
au niveau de l écriture de l équivalence est ce que c est juste de l écrire de cette façon et ou est la faute
z' est rée si et seulement si z'=0 ou z'est différent de 0 ou argz'= o ou pi mod 2pi
est possible de me traiter le cas de z' imaginaire pur ou imaginaire avec les arguments
Non, ce que tu écris est faux :
Déjà, si tu mets "
(en mathématique, dire "ou" c'est parler d'une réunion d'ensemble : "
Retiens que "
Autrement dit,
Commence par regarder et travailler le cas imaginaire avant de me demander un coup de main :lol3:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
modification des conditions
[quote="capitaine nuggets"]
merci pour les explications
voici les définitions qu on utilise si possible de les rectifier ( j ai ajouté (et) dans la deuxième partie
z'réel" si et seulement si "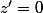 ou (
ou ( et argz'=kpi )
et argz'=kpi )
z'est imaginaire " si et seulement si "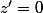 ou (
ou ( et argz'=kpi/2 )
et argz'=kpi/2 )
donc l ensemble est un cercle privé seulement du point B
merci
merci pour les explications
voici les définitions qu on utilise si possible de les rectifier ( j ai ajouté (et) dans la deuxième partie
z'réel" si et seulement si "
z'est imaginaire " si et seulement si "
donc l ensemble est un cercle privé seulement du point B
merci
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
