Nombre de surjection de E dans F

[alexis6]

Bonjour,

Pour deux ensembles finis E et F de cardinaux respectivement n et p ( p < ou = à n ) combien y a t-il de surjection de E dans F. Je note S(n;p) le nombre de surjections de E dans F

S ( n;p ) = C (p;n) * (p ^ (n-p)) ssi n>p
S ( n;p )= n! si n=p

Alors en fait je ne saurais pas l'expliquer formellement, mais je trouve cette formule. En vrai je sais que c'est beaucoup plus compliqué comme formule mais dans ce cas pourriez vous me donner un contre exemple de ma formule SVP?

Merci d'avance!

[Axiom]

Bonjour Alexis6.. :happy:

Effectivement la formule de dénombrement des surjections d'un ensemble vers un autre est assez compliquée à démontrer, mais elle est accessible dès la première année de prépa.... :lol3:

Pour ce qui est de ta formule, je te propose cette idée par exemple :

Soient les deux ensembles : et
Le nombre de surjections de l'ensemble
On a applications possibles, parmi elles, deux seulement sont non surjectives, les applications constantes.
On a alors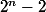 applications surjectives.

Pour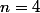 on a pour la formule donnée : possibilités alors que pour ta formule on trouve

Voilà pour un contre-exemple de ta formule.. :lol3:

Si tu veux une démonstration exhaustive, je te conseille d'aller regarder de ce côté, c'est assez abordable, même pour un élève de lycée.. :happy:

=> [url=https://fr.wikiversity.org/wiki/Formule_du_crible/Dénombrement_des_surjections]Surjections[/url]

[jlb]

Salut, merci pour ce lien :we:

[alexis6]

D'abord merci pour la réponse et pour le lien. La formule est mauvaise ( mais elle marche pour n=3 ), le contre-exemple le montre très bien elle foire pour n>3. En fait pour la trouver, j'avais procédé ainsi:

- d'abord trouver toutes les bijections de E' --> F: il y en a C(p;n)
Ou E' inclus dans E et Card(E')=p
- trouver toutes les images des n-p arguments restants: il y en a p^(n-p)

Donc il y a C(p;n)*(p^(n-p)). Sauf que ça ne marche pas parce qu'il y a très vite des répétitions. Par contre si je pouvais " quantifier " avec n et p les répétitions je pourrais retrouver la formule. Mais bon j'y arriverai pas. Je vais regarder le lien.