Bonjour, je suis actuellement « bloqué » sur mon exercice de devoir maison... On m’a demandé de chercher le nombre d’or « phi » d’un rectangle (la longueur) à partir d’une équation xcarré-x-1=0 si ça peut servir; le résultat obtenu est (1+racine de 5)/2.
On m’a demandé de montrer que « phi »carré=« phi »+1. Je l’ai donc montré par des calculs.
Désormais, on me demande de déterminer deux entiers a et b tel que « phi »au cube=a* « phi »+b. J’aurai pu dire que a et b était égaux à « phi », mais on me demande des nombres entiers... J’ai trouvé que ça marchait pour a=2 et b=1... Mais je n’arrive pas du tout à le démontrer! Pouvez vous m’aider svp...
Ensuite je dois montrer que 1/«phi »=« phi »-1; comment puis-je démontrer cette vérité par des calculs?
Pour finir, ma dernière question est celle du dernier exercice, je dois déterminer deux entiers a et b à nouveau, mais pour que 1/« phi »carré=a* « phi »+b...
Un grand merci pour votre aide
Nombre D’or, devoir maion
13 messages
- Page 1 sur 1
Re: Nombre D’or, devoir maion
Bonjour
tu sais que
donc \times (\phi + 1)=\dots[/tex]
\times (\phi + 1)=\dots[/tex]
vois-tu ?
tu sais que
donc
vois-tu ?
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Nombre D’or, devoir maion
oups...
vam a écrit:Bonjour
tu sais que
donc
vois-tu ?
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Nombre D’or, devoir maion
jour,
Pour le cube : puisque , il faut calculer
, il faut calculer  c'est-à-dire
c'est-à-dire
^3)
Deux choses : (1) quand une fraction est élevée à une certaine puissance, que peut-on dire du numérateur et du dénominateur et (2) comment faire pour calculer de façon générale^3) ?
?
Pour l'inverse : deux méthodes.
La première : pour démontrer que , il suffit de montrer que
, il suffit de montrer que 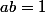
On utilise cette méthode quand on connaît a et b.
La seconde : de façon générale, la "forme conjuguée" de) , c'est
, c'est ) car quand on multiplie cela fait
car quand on multiplie cela fait 
C'est très pratique dans une fraction quand il y a des racines carrées : car on peut multiplier numérateur ET dénominateur par la quantité conjuguée sans changer le nombre.
Exemple avec
(\sqrt{2}+1)}=\dfrac{\sqrt{2}+1}{2-1}=\sqrt{2}+1)
vous pouvez vous entraîner avec la même technique sur le nombre d'or.
Pour le cube : puisque
Deux choses : (1) quand une fraction est élevée à une certaine puissance, que peut-on dire du numérateur et du dénominateur et (2) comment faire pour calculer de façon générale
Pour l'inverse : deux méthodes.
La première : pour démontrer que
On utilise cette méthode quand on connaît a et b.
La seconde : de façon générale, la "forme conjuguée" de
C'est très pratique dans une fraction quand il y a des racines carrées : car on peut multiplier numérateur ET dénominateur par la quantité conjuguée sans changer le nombre.
Exemple avec
vous pouvez vous entraîner avec la même technique sur le nombre d'or.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Nombre D’or, devoir maion
certes mais le grand intérêt du nombre d'or c'est qu'il est solution de l'équation x²-x-1=0
soit

et delà aucun calcul n'est nécessaire...

soit
et delà aucun calcul n'est nécessaire...
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Nombre D’or, devoir maion
bonsoir,
=..)
 vérifie
vérifie 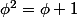
question 2, calcul de 1/phi
on a (*)
(*)
divise les deux membres de l'égalité (*) par
question 2, calcul de 1/phi^2
on a (*)
(*)
divise les deux membres de l'égalité (*) par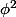
question 2, calcul de 1/phi
on a
divise les deux membres de l'égalité (*) par
question 2, calcul de 1/phi^2
on a
divise les deux membres de l'égalité (*) par
Re: Nombre D’or, devoir maion
Bonjour,
Je vous remercie énormément pour tous vos retours... C’est la première fois que je rencontre le « nombre d’or », c’est pour cela que j’étais un peu perdu....
Pour la première question, c’est bien ce que j’avais réalisé... j’avais trouvé, mais je n’obtiens toujours pas d’entiers pour a et b?
Je vous remercie énormément pour tous vos retours... C’est la première fois que je rencontre le « nombre d’or », c’est pour cela que j’étais un peu perdu....
Pour la première question, c’est bien ce que j’avais réalisé... j’avais trouvé, mais je n’obtiens toujours pas d’entiers pour a et b?
Re: Nombre D’or, devoir maion
mais si...

donc
=\phi ^2 +\phi=(\phi+1)+\phi=2\phi + 1)
donc
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Nombre D’or, devoir maion
Bonjour,
Merci beaucoup, j’avais pas compris dans ce sens là!
Bonne journée
Merci beaucoup, j’avais pas compris dans ce sens là!
Bonne journée
Re: Nombre D’or, devoir maion
et donc tu remarqueras que même ton premier calcul était inutile
le simple fait que soit solution de ton équation permettait de répondre
soit solution de ton équation permettait de répondre

le simple fait que
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Nombre D’or, devoir maion
Pour la dernière question, je dois déterminer les entiers a et b afin que 1/« phi »carré= a* « phi »+b...
Je sais que 1/phi=phi-1... il me suffit de multiplier par 1/phi des deux côtés de l’égalité?
Je sais que 1/phi=phi-1... il me suffit de multiplier par 1/phi des deux côtés de l’égalité?
Re: Nombre D’or, devoir maion
Je reviens vers vous... J’ai une suite définie par F0=1, F1=1 et Fn+2=Fn+1 + Fn.
J’ai calculé les termes jusqu’à F11... Ensuite, pour chaque « n » jusqu’à F10, j’ai calculé (Fn+1)/(Fn).
Arrondi à 10^-3, j’ai obtenu:
F0=1, F1=2, F2=1.5, F3=1.667, F4=1.6, F5=1.625, F6=1.615, F7=1.619, F8=1.618, F9=1.618 et F10=1.618...
Je dois émettre une conjecture pour cette suite de terme général (Fn+1)/(Fn), la seule que j’aurai trouvé aurait été , le résultat est le meme pour tout n supérieur ou égal à 8. Est ce une bonne conjecture ou y en a-t-il une meilleure?
En vous remerciant
J’ai calculé les termes jusqu’à F11... Ensuite, pour chaque « n » jusqu’à F10, j’ai calculé (Fn+1)/(Fn).
Arrondi à 10^-3, j’ai obtenu:
F0=1, F1=2, F2=1.5, F3=1.667, F4=1.6, F5=1.625, F6=1.615, F7=1.619, F8=1.618, F9=1.618 et F10=1.618...
Je dois émettre une conjecture pour cette suite de terme général (Fn+1)/(Fn), la seule que j’aurai trouvé aurait été , le résultat est le meme pour tout n supérieur ou égal à 8. Est ce une bonne conjecture ou y en a-t-il une meilleure?
En vous remerciant
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
