[1ere S] Montrer que A/B+B/A ≥ 2
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
jygl
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Oct 2015, 17:03
-
 par jygl » 06 Nov 2015, 14:48
par jygl » 06 Nov 2015, 14:48
Bonjour tout le monde ! :we:
Voilà, j'ai un petit DM à faire, avec entre autres cet exercice :
[INDENT]Soient
a et b deux réels strictement positifs, montrer que
a/b+b/a  2
2[/INDENT]
Le truc, c'est que c'est évident dans ma tête, mais je ne vois pas comment le
montrer ^^ :mur:
Pourriez-vous me fournir quelques pistes svp ? Merci !

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Nov 2015, 15:16
par Carpate » 06 Nov 2015, 15:16
jygl a écrit:Bonjour tout le monde ! :we:
Voilà, j'ai un petit DM à faire, avec entre autres cet exercice :
[INDENT]Soient
a, b, c et d quatre réels strictement positifs, montrer que
a/b+b/a+c/d+d/c  4
4[/INDENT]
D'où
a/b+b/a  2
2Enfin il me semble...
Le truc, c'est que c'est évident dans ma tête, mais je ne vois pas comment le
montrer ^^ :mur:
Pourriez-vous me fournir quelques pistes svp ? Merci !

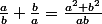
^2=a^2+b^2-2ab)
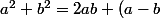^2)
^2}{ab} \geq2)
car
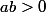
égalité pour

-
jygl
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Oct 2015, 17:03
-
 par jygl » 06 Nov 2015, 15:20
par jygl » 06 Nov 2015, 15:20
Haha je ne demandais spécialement la réponse !

Mais merci beaucoup, je vais y songer ! :we:

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 06 Nov 2015, 20:49
par zygomatique » 06 Nov 2015, 20:49
salut
JFF ...
a et b sont positifs donc a/b et b/a sont positifs ...
or tout nombre positif est le carré de sa racine carré
donc
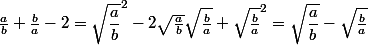^2)
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
jygl
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Oct 2015, 17:03
-
 par jygl » 06 Nov 2015, 20:59
par jygl » 06 Nov 2015, 20:59
zygomatique a écrit:salut
JFF ...
a et b sont positifs donc a/b et b/a sont positifs ...
or tout nombre positif est le carré de sa racine carré
donc
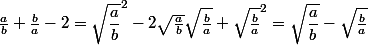^2)
:zen:
Haha merci pour ta réponse ^^
Mais j'ai des "problèmes" pour passer de quelque chose comme ce que tu m'as proposé (
^2)
) à la conclusion... :/ :mur:

PS : ne m'en voulez pas trop il se fait tard... :dodo:

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 06 Nov 2015, 21:20
par Sake » 06 Nov 2015, 21:20
Salut,
jygl a écrit:Haha merci pour ta réponse ^^
Mais j'ai des "problèmes" pour passer de quelque chose comme ce que tu m'as proposé (
^2)
) à la conclusion... :/ :mur:

PS : ne m'en voulez pas trop il se fait tard... :dodo:
Il faut revenir pour cela au début du calcul. Pourquoi Zygo a-t-il calculé a/b + b/a - 2 ? Il y a en fait une raison à cela : On voit que le terme
^2)
est positif, car il s'agit d'un carré, donc a/b + b/a - 2 est positif, d'où la conclusion.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 07 Nov 2015, 08:05
par Carpate » 07 Nov 2015, 08:05
zygomatique a écrit:salut
JFF ...
a et b sont positifs donc a/b et b/a sont positifs ...
or tout nombre positif est le carré de sa racine carré
donc
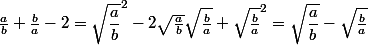^2)
:zen:
C'est la même chose, sans radical, que :
^2}{ab})
qui découle directement de l'identité remarquable
^2)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 07 Nov 2015, 09:58
par zygomatique » 07 Nov 2015, 09:58
oui l'idée primaire est la même ... mais le cheminement n'est pas du tout le même ...
mon cheminement est la classique application de la règle classique :: pour comparer deux nombres on étudie le signe de leur différence ....
remarquer tout de même que a/b et b/a sont inverses et (x + 1/x)^2 = ....
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
jygl
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Oct 2015, 17:03
-
 par jygl » 07 Nov 2015, 12:29
par jygl » 07 Nov 2015, 12:29
zygomatique a écrit:oui l'idée primaire est la même ... mais le cheminement n'est pas du tout le même ...
mon cheminement est la classique application de la règle classique :: pour comparer deux nombres on étudie le signe de leur différence ....
remarquer tout de même que a/b et b/a sont inverses et (x + 1/x)^2 = ....
...
Merci à vous deux encore pour vos réponses !
J'ai encore un peu de chemin à faire avant d'en arriver à trouver cela tout seul, mais bon... Merci beaucoup !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 07 Nov 2015, 15:23
par Carpate » 07 Nov 2015, 15:23
zygomatique a écrit:oui l'idée primaire est la même ... mais le cheminement n'est pas du tout le même ...
mon cheminement est la classique application de la règle classique :: pour comparer deux nombres on étudie le signe de leur différence ....
remarquer tout de même que a/b et b/a sont inverses et (x + 1/x)^2 = ....
...
Mais pourquoi passer par les radicaux ? alors que comparer 1/a+1/b et 2 fait directement intervenir le terme (a-b)^2

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 07 Nov 2015, 15:37
par Sake » 07 Nov 2015, 15:37
Carpate a écrit:Mais pourquoi passer par les radicaux ? alors que comparer 1/a+1/b et 2 fait directement intervenir le terme (a-b)^2
Bah peu importe, franchement...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 07 Nov 2015, 22:35
par zygomatique » 07 Nov 2015, 22:35
Carpate a écrit:Mais pourquoi passer par les radicaux ? alors que comparer 1/a+1/b et 2 fait directement intervenir le terme (a-b)^2
ben parce que la différence est une identité remarquable .... :lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 08 Nov 2015, 11:15
par Shew » 08 Nov 2015, 11:15
jygl a écrit:Bonjour tout le monde ! :we:
Voilà, j'ai un petit DM à faire, avec entre autres cet exercice :
[INDENT]Soient
a et b deux réels strictement positifs, montrer que
a/b+b/a  2
2[/INDENT]
Le truc, c'est que c'est évident dans ma tête, mais je ne vois pas comment le
montrer ^^ :mur:
Pourriez-vous me fournir quelques pistes svp ? Merci !

Bonjour
^2}{ab} + 2)
Comme
^2 \ge 0)
(le carré d'un nombre est toujours positif)
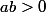
(d'après l'énoncé a et b sont deux réels positifs donc leur produit est aussi positif) donc :
^2}{ab} \ge 0)
^2}{ab} + 2 \ge 2)
soit par substitution :
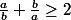
-
tototo
- Membre Rationnel
- Messages: 954
- Enregistré le: 08 Nov 2011, 07:41
-
 par tototo » 09 Nov 2015, 16:53
par tototo » 09 Nov 2015, 16:53
Bonjour tout le monde ! :we:
Voilà, j'ai un petit DM à faire, avec entre autres cet exercice :
[INDENT]Soient
a et b deux réels strictement positifs, montrer que
a/b+b/a  2
2[/INDENT]
(a^2+b^2)/ab-2ab/ab>=0
(a-b)^2/ab> .. 0
Un carre etant toujour superieur a zero ainsi que le produit de deux nombre > 0. Donc on a demontrer .
Le truc, c'est que c'est évident dans ma tête, mais je ne vois pas comment le
montrer ^^ :mur:
Pourriez-vous me fournir quelques pistes svp ? Merci !

[/quote]
-
Paul1
- Messages: 4
- Enregistré le: 03 Nov 2015, 09:40
-
 par Paul1 » 10 Nov 2015, 13:24
par Paul1 » 10 Nov 2015, 13:24
Salut!
(a-b)² ;) 0
a²-2ab+b² ;) 0
a²-b²;)2ab
On simplifie par ab
a²/ab - b²/ab ;)2ab/ab
a/b - b/a ;)2
:lol3:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Nov 2015, 18:19
par Carpate » 10 Nov 2015, 18:19
tototo a écrit:Bonjour tout le monde ! :we:
Voilà, j'ai un petit DM à faire, avec entre autres cet exercice :
[INDENT]Soient
a et b deux réels strictement positifs, montrer que
a/b+b/a  2
2[/INDENT]
(a^2+b^2)/ab-2ab/ab>=0
(a-b)^2/ab> .. 0
Un carre etant toujour superieur a zero ainsi que le produit de deux nombre > 0. Donc on a demontrer .
Le truc, c'est que c'est évident dans ma tête, mais je ne vois pas comment le
montrer ^^ :mur:
Pourriez-vous me fournir quelques pistes svp ? Merci !

tototo a encore frappé !
-
t0hierry
- Messages: 1
- Enregistré le: 16 Sep 2021, 06:17
-
 par t0hierry » 16 Sep 2021, 06:26
par t0hierry » 16 Sep 2021, 06:26
(a - b)^2 >= 0
(a^2 + b^2 - 2ab) >= 0
(a^2 + b^2) >= 2ab
(a/b + b/a) >=2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
