X⁶ -x⁵ +x⁴ -x³ +x² -x +1≥½
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zarlino1
- Messages: 6
- Enregistré le: 09 Nov 2015, 19:52
-
 par zarlino1 » 09 Nov 2015, 20:01
par zarlino1 » 09 Nov 2015, 20:01
Bonjour,
montrer que
x;) -x;) +x;) -x³ +x² -x +1;)½
pour tout x de R
bon
j ai calcule la différence et essaye de mettre en évidence des identités ....
merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 09 Nov 2015, 20:05
par zygomatique » 09 Nov 2015, 20:05
salut
ne reconnais-tu donc rien dans ce premier membre ?
et l'énoncé est-il complet ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
zarlino1
- Messages: 6
- Enregistré le: 09 Nov 2015, 19:52
-
 par zarlino1 » 09 Nov 2015, 20:10
par zarlino1 » 09 Nov 2015, 20:10
zygomatique a écrit:salut
ne reconnais-tu donc rien dans ce premier membre ?
et l'énoncé est-il complet ?
Merci pour la remarque
on montre pour tout x de R

;)R
x;)-x;)+x;) -x³ +x² -x +1;)½
merci
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 09 Nov 2015, 20:51
par Carpate » 09 Nov 2015, 20:51
zarlino1 a écrit:Bonjour,
montrer que
x;) -x;) +x;) -x³ +x² -x +1;)½
pour tout x de R
bon
j ai calcule la différence et essaye de mettre en évidence des identités ....
merci
L'étude de la fonction
=x^6-x^5+x^4-x^3+x^2-x+1)
et notamment du signe de sa dérivée se simplifie en considérant f comme la somme des 7 termes de la progression géométrique de premier terme 1 et de raison -x
-
zarlino1
- Messages: 6
- Enregistré le: 09 Nov 2015, 19:52
-
 par zarlino1 » 09 Nov 2015, 21:10
par zarlino1 » 09 Nov 2015, 21:10
Carpate a écrit:L'étude de la fonction
=x^6-x^5+x^4-x^3+x^2-x+1)
et notamment du signe de sa dérivée se simplifie en considérant f comme la somme des 7 termes de la progression géométrique de premier terme 1 et de raison -x
Merci
mais on a pas encore fait derive
juste technique de base identite majoration etc
leçon porte sur inégalité ordre
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 09 Nov 2015, 21:23
par Carpate » 09 Nov 2015, 21:23
zarlino1 a écrit:Merci
mais on a pas encore fait derive
juste technique de base identite majoration etc
leçon porte sur inégalité ordre
Et les séries géométriques, vous avez vu ?
-
zarlino1
- Messages: 6
- Enregistré le: 09 Nov 2015, 19:52
-
 par zarlino1 » 09 Nov 2015, 21:41
par zarlino1 » 09 Nov 2015, 21:41
Carpate a écrit:Et les séries géométriques, vous avez vu ?
oui
jai factorise comme ceci (1 +x;));)(1+x);)½
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 09 Nov 2015, 21:44
par Carpate » 09 Nov 2015, 21:44
zarlino1 a écrit:oui
jai factorise comme ceci (1 +x;));)(1+x);)½
Oui, c'est ce que donne


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Nov 2015, 21:59
par chan79 » 09 Nov 2015, 21:59
salut
il faut montrer

(x^2-x+1)\geq -0.5)
on encadre chaque facteur

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 09 Nov 2015, 21:59
par Lostounet » 09 Nov 2015, 21:59
Je suis curieux de voir la suite :ptdr:
Car la dérivée n'est pas jolie.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
zarlino1
- Messages: 6
- Enregistré le: 09 Nov 2015, 19:52
-
 par zarlino1 » 09 Nov 2015, 22:02
par zarlino1 » 09 Nov 2015, 22:02
chan79 a écrit:salut
il faut montrer

(x^2-x+1)\geq -0.25)
on encadre chaque facteur
merci
mais
d abord c est -0.5 et non -0.25
de plus on n a pas de condition sur x pour tout x

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Nov 2015, 22:08
par chan79 » 09 Nov 2015, 22:08
zarlino1 a écrit: c' est -0.5 et non -0.25
oui, je viens de corriger
le second facteur est toujours positif
le premier est négatif seulement pour

entre 0 et 1
il faut encadrer

pour

entre 0 et 1
on peut montrer

pour

entre 0 et 1, ce qui montre l'inégalité

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Nov 2015, 10:40
par chan79 » 10 Nov 2015, 10:40
je reprends
il faut montrer
(x^2-x+1)\geq -0,5)
on suppose
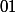
ou
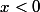
)
on a

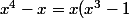=x(x-1)(x^2+x+1))

est négatif si

est entre 0 et 1
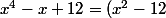^2+(x-\fra{1}{2})^2)
cela donne


on a donc:


en multipliant:
(x^2-x+1)|\leq \fra{1}{2})
donc
(x^2-x+1) \leq \fra{1}{2})
l'inégalité de gauche donne le résultat
à vérifier ...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Nov 2015, 20:08
par zygomatique » 10 Nov 2015, 20:08
 = x^6 - x^5 + x^4 - x^3 + x^2 - x + 1)
on veut montrer que f(x) >= 1/2
1/ si
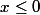
c'est évident : les termes sont positifs et l'un est 1 ....
2/ soit
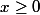
posons
 = 2f(x) - 1 = 2x^7 + 1 - x)
il faut montrer que
 \ge 0)
si
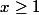
c'est évident car

si
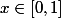
alors

et

donc
 \ge 0)
on a donc le résultat ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Nov 2015, 20:17
par chan79 » 10 Nov 2015, 20:17
zygomatique a écrit:posons
 = 2f(x) - 1 = 2x^7 + 1 - x)
bien vu, mais il doit y avoir un dénominateur pour g(x)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Nov 2015, 20:55
par zygomatique » 10 Nov 2015, 20:55
oui tu as raison ....
il doit y avoir x + 1 ... mais qui est positif quand x >= 0 donc ne fausse pas le raisonnement ....
il me semble ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
zarlino1
- Messages: 6
- Enregistré le: 09 Nov 2015, 19:52
-
 par zarlino1 » 11 Nov 2015, 01:37
par zarlino1 » 11 Nov 2015, 01:37
zygomatique a écrit: = x^6 - x^5 + x^4 - x^3 + x^2 - x + 1)
on veut montrer que f(x) >= 1/2
1/ si
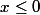
c'est évident : les termes sont positifs et l'un est 1 ....
2/ soit
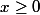
posons
 = 2f(x) - 1 = 2x^7 + 1 - x)
il faut montrer que
 \ge 0)
si
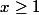
c'est évident car

si
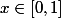
alors

et

donc
 \ge 0)
on a donc le résultat ...
:lol3:
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
et notamment du signe de sa dérivée se simplifie en considérant f comme la somme des 7 termes de la progression géométrique de premier terme 1 et de raison -x
