Modulo

[mcfit]

Bonjour j'ai un exercice de spé maths et je suis bloqué sur un exercice:
Soit N=a indice n, a indice n-1...a indice2, a indice1, a indice 0 un nombre entier(a indice 0 est le chiffre des unités, a indice1 celui des dizaines etc...)

1)Ecrire N à l'aide de puissances de 10 et des chiffres a indice 0, a indice 1... a indice n.
2))En déduire la congruence module 9 du nombre N.
3)En déduire le critère de divisibilité par 9 d'un nombre entier.

Merci beaucoup pour votre aide.

[lyceen95]

Ok. Et tu as fait quoi, ça t'inspire quoi ?

Si j'écris le nombre 64 par exemple, 64 = 6 dizaines + 4 unités, n'est-ce pas ? 305 , c'est 3 centaines et 5 unités. Voilà... c'est ça le thème de l'exercice. A toi de jouer.

[mcfit]

Oui mais comment on peut écrire le nombre N avec des puissances de 10 et de a indice 0 ...?

[titine]

Ok. Et tu as fait quoi, ça t'inspire quoi ?

Si j'écris le nombre 64 par exemple, 64 = 6 dizaines + 4 unités, n'est-ce pas ? 305 , c'est 3 centaines et 5 unités. Voilà... c'est ça le thème de l'exercice. A toi de jouer.

Je dirai même plus : 305 = 5*10^0 + 0*10^1 + 3*10^2 !

[mcfit]

Merci titine mais comment fait on cela avec N?

[mcfit]

N = 10 puissance??? combien de dizaines combien d'unités?? Je n'arrive pas à commencer.

[titine]

Bin pareil !
N s'écrit a_n a_n-1 ..... a_2 a_1 a_0
Par exemple si N = 5324 on a a_0 = 4 , a_1 = 2 , a_3 = 3 ...
Et N = 4*10^0 + 2*10^1 + 3*10^3 + 5*10^4

[lyceen95]

Une unité, c'est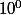
Une dizaine ou dix, c'est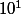
Une centaine ou cent, c'est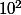
Un millier c'est ?

[aymanemaysae]

Bonjour ;

Les nombres communément utilisés sont des nombres écrits selon le système de numération à base , qui est un système au moyen duquel on représente les nombres avec symboles : .

Un exemple vaut mieux qu'un long discours , donc on va étudier un exemple .

On a un nombre , par exemple ;

donc .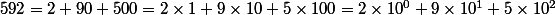

On voit que chaque terme de cette addition est un produit de deux facteurs dont l'un est une puissance de 10 .

C'est de là que vient l'appellation : système de numération à base .

On peut avoir un système de numération à base : c'est le système binaire ;

un système de numération à base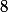 : c'est le système octal ;

un système de numération à base : c'est le système décimal ;

un système de numération à base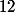 : c'est le système duodécimal ;

un système de numération à base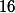 : c'est le système hexadécimal ;

un système de numération à base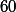 : c'est le système sexagésimal ; etc .... .


Ce qu'il faut retenir , c'est que dans le système de numération à base , tout nombre entier naturel s'écrit comme suit : avec 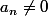sans oublier que tous les .