Module et argument
13 messages
- Page 1 sur 1
Module et argument
Bonjour chers collegues
Je n'arrive pas a démarrer cet exercice de rentrée en PCSI :cry: et donc je vous prie s'il vous plaît de bien voilair m'aider
Il faut que je trouve l'argument et le module de
[1+cos(x)+i sin(x) ]/ [1 + cos(x) -i sin(x)]
Merci de votre réponse .
Je n'arrive pas a démarrer cet exercice de rentrée en PCSI :cry: et donc je vous prie s'il vous plaît de bien voilair m'aider
Il faut que je trouve l'argument et le module de
[1+cos(x)+i sin(x) ]/ [1 + cos(x) -i sin(x)]
Merci de votre réponse .
Ryuk a écrit:Bonjour chers collegues
Je n'arrive pas a démarrer cet exercice de rentrée en PCSIet donc je vous prie s'il vous plaît de bien voilair m'aider
Il faut que je trouve l'argument et le module de
[1+cos(x)+i sin(x) ]/ [1 + cos(x) -i sin(x)]
Merci de votre réponse .
Bonjour,
Ne seraient-ce point deux complexes conjugués?
Ryuk a écrit:Bonjour chers collegues
Je n'arrive pas a démarrer cet exercice de rentrée en PCSIet donc je vous prie s'il vous plaît de bien voilair m'aider
Il faut que je trouve l'argument et le module de
f(x)=[1+cos(x)+i sin(x) ]/ [1 + cos(x) -i sin(x)]
Merci de votre réponse .
bonjour,
tu dois te familiariser avec la notation d'Euler,ie, l'exponentielle
complexe.
la notation
de trigo possibles et inimaginables à un seul calcul d'exposant:
voiçi ce que cela donne dans le cas présent:
on met en facteur l'exponentielle de l'arc moitié
bonjour,
il faudrait que tu te rendes compte des choses par toi-même,
sans que l'on balance un résultat
voilà ce qu'il y a à démontrer
1) l'équation admet trois solutions complexes.
admet trois solutions complexes.
écris leurs forme trigo et leur forme cartésienne des trois racines
en calculant)
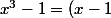 \times ..)
puis trinôme du second degré
2)
on pose
que vaut ?
?
montre que l'autre racine est
3) déduis en la valeur de
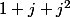
(suite géométrique ou bien 1+2Re(j))
il faudrait que tu te rendes compte des choses par toi-même,
sans que l'on balance un résultat
voilà ce qu'il y a à démontrer
1) l'équation
écris leurs forme trigo et leur forme cartésienne des trois racines
en calculant
puis trinôme du second degré
2)
on pose
que vaut
montre que l'autre racine est
3) déduis en la valeur de
(suite géométrique ou bien 1+2Re(j))
Ryuk a écrit:je ne savais pas à quoi j correspondait , on me l'a pas appris il fallait juste me dire que j etait égal a ce que vous avez dit et de je ne vois pas le rapport avec ce que vous avec dit et module de (1+j)^2n
je répète: c'est bien pour cela que je te propose mon exercice.
des résultats à son sujet, à connaitre.
donne-moi la forme cartésienne de j. comment l'obtient-on ?
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
