Ce que tu as pour le moment, c'est donc ça :
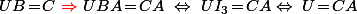
(ou seul le truc en rouge n'est pas une équivalence)
Et arrivé à ce point, tu as plusieurs solutions :
- Soit tu reste pragmatique et tu dit que l'implication en question, ce qu'elle dit, c'est que, si U est une solution de l'équation UB=C, alors forcément U=CA. Donc ce que ça te dit, c'est que
la seule éventuelle solution de l'équation UB=C, c'est U=CA et pour savoir si effectivement c'est bien une solution,, ben il suffit de calculer la matrice U=CA puis de regarder si c'est vrai ou pas qu'on a UB=C pour cette matrice U là.
- Soit tu veut rester "un peu théorique" et tu peut te dire que, de la même façon qu'on a "enlevé le B" dans l'équation UB=C en multipliant à droite par A, ben on peut "enlever le A" dans l'équation U=CA en multipliant à droite par B :
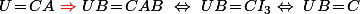
Vu que les question précédentes te disent que, non seulement on a

, mais on a aussi

.
Remarque : Et en fait, tout cela provient du fait que la matrice A est "inversible" (notion qui n'est visiblement pas au programme de ton année) et que son inverse, c'est la matrice B.
Et ce qu'on vient de faire, c'est la même chose que dans

où on a

: pour l'implication
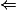
, on multiplie par

les deux cotés de l'équation et, pour l'implication

, on multiplie par

(c'est à dire l'inverse de 3) les deux cotés de l'équation. La seule (grosse) différence avec les matrice, c'est que dans les réels sont tous inversible sauf le réel 0, alors que pour les matrices, c'est bien plus compliqué : il y a des tas de matrices qui ne sont pas inversible (par exemple la matrice A de mon précédent post).




