DM maths
17 messages
- Page 1 sur 1
DM maths
Je rencontre um problème sur un exercice que voici :
u_{n}=\frac{1}{n^2}+\frac{2}{n^2}+...+\frac{n}{n^2}
logiciel ne fonctionne pas
Sa semble tendre vers 0,5
La question est de determiner la limite de u.
Merci d'avance
u_{n}=\frac{1}{n^2}+\frac{2}{n^2}+...+\frac{n}{n^2}
logiciel ne fonctionne pas
Sa semble tendre vers 0,5
La question est de determiner la limite de u.
Merci d'avance
Re: DM maths
tu met 1/n² en facteur
tu reconnait somme connue somme (i) pour i=1 à n
tu étudie la limite
soit f(x)=x
tu met 1/n en facteur
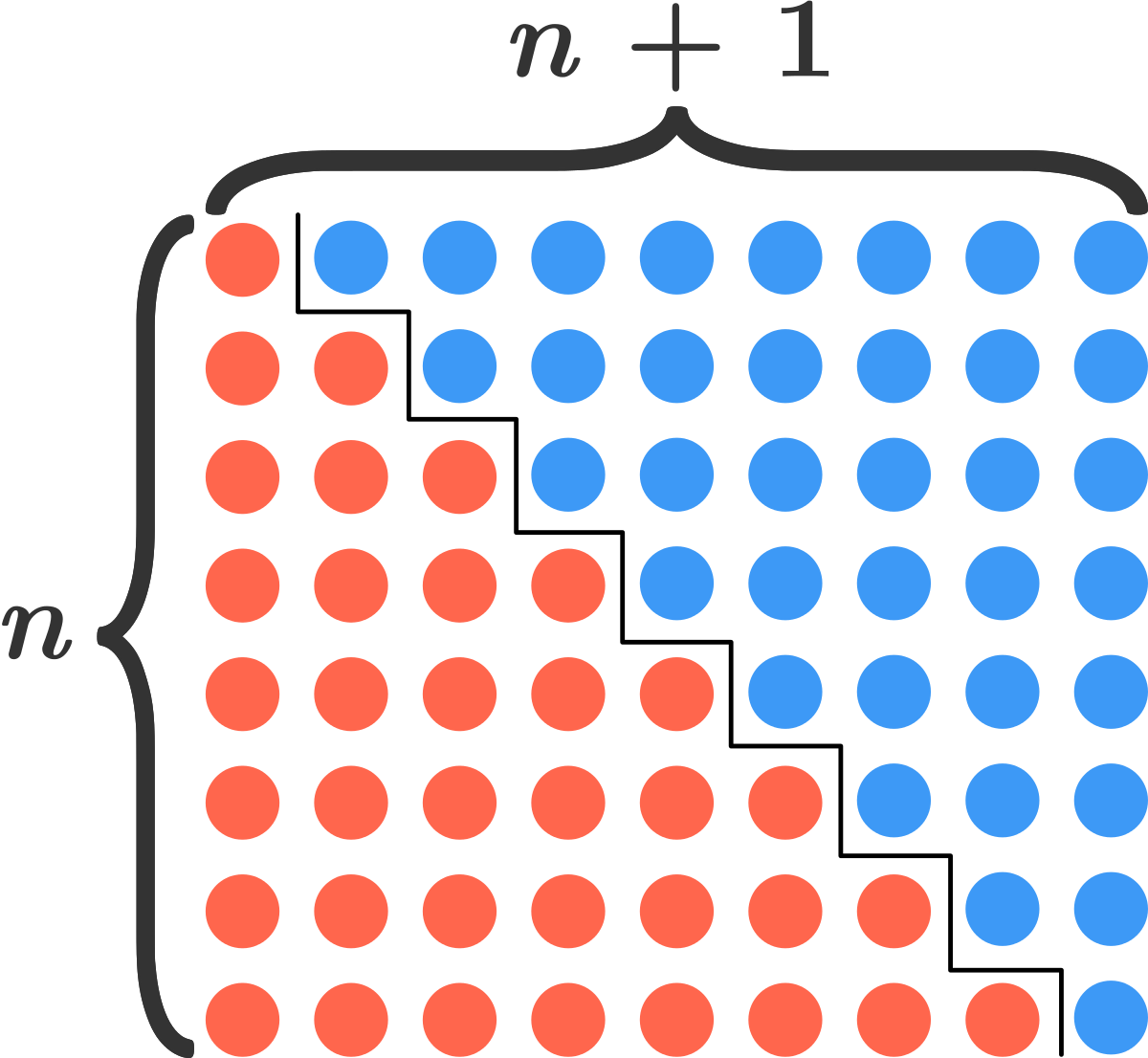
tu reconnais une approximation par exès, par la méthode des rectangles de l'intégrale de f(x) entre 0 et 1
tu reconnait somme connue somme (i) pour i=1 à n
tu étudie la limite
soit f(x)=x
tu met 1/n en facteur
tu reconnais une approximation par exès, par la méthode des rectangles de l'intégrale de f(x) entre 0 et 1
Re: DM maths
Je n'ai pas encore abordé la méthode des rectangle mais merci infiniment pour cette rapidité.
Or la simplification par 1/n^2 donne
0*infini
Or ceci est une forme indéterminée.
Or la simplification par 1/n^2 donne
0*infini
Or ceci est une forme indéterminée.
Re: DM maths
bonjour,
on a

dans le cours d'intégration on sait que , pour continue:
continue:
dx = \lim_{n \rightarrow +\infty} \sum_{k=1}^n \, \dfrac{1}{n} f(\dfrac{k}{n}))
d'où
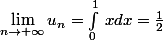
on a
dans le cours d'intégration on sait que , pour
d'où
Modifié en dernier par mathelot le 09 Oct 2018, 17:30, modifié 2 fois.
Re: DM maths
EstebanBrlg a écrit:Je n'ai pas encore abordé la méthode des rectangle mais merci infiniment pour cette rapidité.
Or la simplification par 1/n^2 donne
0*infini
Or ceci est une forme indéterminée.
Maintenant, que vaut
Edit : Sinon Ben va me taper
Re: DM maths
Vous serez sûrement choqué de mon niveau or je ne comprend pas cette écriture et cette démarche
Re: DM maths
EstebanBrlg a écrit:Vous serez sûrement choqué de mon niveau or je ne comprend pas cette écriture et cette démarche
Voilà maintenant tu le sais pour l'éternité.
Re: DM maths
Du coup
E bizzar* k est égal à plus l'infini mais que vaut
(1/n^2)*E bizzar* k et comment trouver ceci ?
E bizzar* k est égal à plus l'infini mais que vaut
(1/n^2)*E bizzar* k et comment trouver ceci ?
Re: DM maths
soit 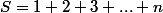
on réécrit la somme
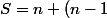+..+2+1)
d'où en additionnant les deux égalités
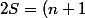+(n+1)+....+(n+1))
d'où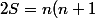)
d'où en divisant par 2
}{2})
signification du signe (la lettre S majuscule en grec)
(la lettre S majuscule en grec)
c'est un opérateur qui signifie qu'on va faire la somme de quantités qui dépendent d'un indice:

on additionné les termes en k^2 en faisant varier k de 1 à n
on réécrit la somme
d'où en additionnant les deux égalités
d'où
d'où en divisant par 2
signification du signe
c'est un opérateur qui signifie qu'on va faire la somme de quantités qui dépendent d'un indice:
on additionné les termes en k^2 en faisant varier k de 1 à n
Modifié en dernier par mathelot le 09 Oct 2018, 17:52, modifié 2 fois.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :