Bonjour,
J'ai un Dm a rendre pour lundi 13 mars, mais le problème est que je ne comprends rien au Dm en question malgré mon cours.
Si quelqu'un aurait la gentillesse de m'aider assez clairement ce serait vraimment génial. Merci d'avance.
Le Dm :
http://img4.hostingpics.net/pics/406182 ... 147844.jpg
Dm de Maths sur les vecteurs
12 messages
- Page 1 sur 1
Re: Dm de Maths sur les vecteurs
bonjour,
si tu ne comprends rien au DM, nous ne comprenons rien .... à la maniere dont on puisse t'aider (a part faire le DM pour toi!)
Qu'est ce que tu ne comprends pas?
Qu'as tu fait?
les coordonnees de C' et B' ?
si tu ne comprends rien au DM, nous ne comprenons rien .... à la maniere dont on puisse t'aider (a part faire le DM pour toi!)
Qu'est ce que tu ne comprends pas?
Qu'as tu fait?
les coordonnees de C' et B' ?
Re: Dm de Maths sur les vecteurs
Bonjour,
On t'aide mais il faut aussi que tu t'aide toi-même en nous écrivant également quelque chose pour que l'on avance ensemble, comprends-tu ? . . . :
2)

avec la définition maintenant (que tu peux également récupérer sur le net) il t'es facile de déterminer les coordonnées de B' et C', non . . . ?
On t'aide mais il faut aussi que tu t'aide toi-même en nous écrivant également quelque chose pour que l'on avance ensemble, comprends-tu ? . . . :
2)

avec la définition maintenant (que tu peux également récupérer sur le net) il t'es facile de déterminer les coordonnées de B' et C', non . . . ?
Re: Dm de Maths sur les vecteurs
siger a écrit:bonjour,
si tu ne comprends rien au DM, nous ne comprenons rien .... à la maniere dont on puisse t'aider (a part faire le DM pour toi!)
Qu'est ce que tu ne comprends pas?
Qu'as tu fait?
les coordonnees de C' et B' ?
Ce que je ne comprends pas c'est un peu tout le début du Dm . La question 1 je ne sais pas la formule pour trouver les coordonnés du point M en utilisant des vecteurs
Re: Dm de Maths sur les vecteurs
Pour t'aider dans la 1 :
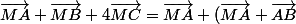+4 (\vec {MA}+\vec{AC}))
et tu n'auras plus que MA en fonction de vecteurs connus.
Tu écris AM= ....
et donc M est le translaté de A de vecteur ...
Variante, avec l'égalité de départ, tu poses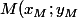) et tu fais un gros système qui te donne
et tu fais un gros système qui te donne 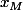 et
et 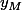
et tu n'auras plus que MA en fonction de vecteurs connus.
Tu écris AM= ....
et donc M est le translaté de A de vecteur ...
Variante, avec l'égalité de départ, tu poses
Re: Dm de Maths sur les vecteurs
Merci du tuyau, je ne peux actuellement pas réfléchir dessus mais en fin d'aprem' je serais dessus
Re: Dm de Maths sur les vecteurs
re
il n'y a pas de formule miracle!
les coordonnees d'un vecteur sont obtenues par la projection de celui-ci sur les axes d'un repere ....
Soit O l'origine du repere
MA+MB+4MC= MO + OA + MO + OB + 4MO + 4OC = 0
d'ou 6OM = OA + OB + 4OC
ou
6xM= xA + xB + 4xC
6yM= yA + yB + 4yC
....
M est sur CC' si C, C' et M sont alignes
lorsque trois point M,N et P sont alignes on peut ecrire
MP = k*NP (par exemple)
c'est a dire que les coordonnees des vecteurs MP et NP sont proportionnelles
(yP-yM)/(xP-xM) = k*(yP-yM)/(xP-xM)
.....
il n'y a pas de formule miracle!
les coordonnees d'un vecteur sont obtenues par la projection de celui-ci sur les axes d'un repere ....
Soit O l'origine du repere
MA+MB+4MC= MO + OA + MO + OB + 4MO + 4OC = 0
d'ou 6OM = OA + OB + 4OC
ou
6xM= xA + xB + 4xC
6yM= yA + yB + 4yC
....
M est sur CC' si C, C' et M sont alignes
lorsque trois point M,N et P sont alignes on peut ecrire
MP = k*NP (par exemple)
c'est a dire que les coordonnees des vecteurs MP et NP sont proportionnelles
(yP-yM)/(xP-xM) = k*(yP-yM)/(xP-xM)
.....
Re: Dm de Maths sur les vecteurs
1)Donc les coordonees de M sont (6;6)
2) J'ai trouvé (3;6) pour les coordonnées des milieux B' et C' des segments [AC] et [AB]
Je suis en train de faire le 3
2) J'ai trouvé (3;6) pour les coordonnées des milieux B' et C' des segments [AC] et [AB]
Je suis en train de faire le 3
Re: Dm de Maths sur les vecteurs
Par contre je ne comprends pas la 3 a ) où il est demandé de remonter que M appartient à la médiane (CC') du triangle A B C il faut calculer les coordonnés de AB et de AC ?
Re: Dm de Maths sur les vecteurs
pascal16 a écrit:xA + xB + 4xC=-2 + 0 + 4*5 = 18
xM=18/6 = 3 pour moi
Désolé j'ai fait une faute d'étourderie
Donc c'est bien (18;6)
Re: Dm de Maths sur les vecteurs
re
xM=(1/6)*(-2+0+20) = 18/6=3
yM=(1/6)*(0+4+8)=12/6=2
d'ou M(3,2)
si M appartient a CC' , alors C,C' et M sont alignes (deja signalé)
on a yC=yC'=yM=2 donc les trois points sont sur une horizontale d'ordonnee 2
xC'<xM<xC donc M est entre C et C'
on doit avoir OM=k*OB' c'est a dire yOM/xOM = yOB'/xOB'
.......
sauf erreur le point J n'est pas defini!
xM=(1/6)*(-2+0+20) = 18/6=3
yM=(1/6)*(0+4+8)=12/6=2
d'ou M(3,2)
si M appartient a CC' , alors C,C' et M sont alignes (deja signalé)
on a yC=yC'=yM=2 donc les trois points sont sur une horizontale d'ordonnee 2
xC'<xM<xC donc M est entre C et C'
on doit avoir OM=k*OB' c'est a dire yOM/xOM = yOB'/xOB'
.......
sauf erreur le point J n'est pas defini!
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
