ABC est un triangle isocèle en A tel que BC = 12
H est le pied de la hauteur issue de A et AH = 9
P et Q sont deux points de [BC] symétriques par rapport a H, on note HP = HQ = x
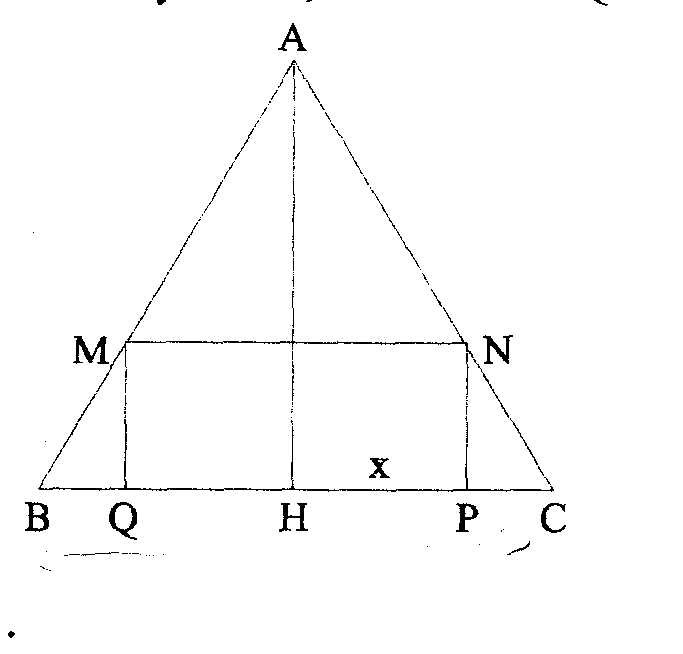
On se pose de déterminer les dimensions du rectangle MNQP d'aire maximale inscrit dans ce triangle.
1.a) Démontrer MQ = (18-3x)/2
> Réponse trouvée
Dans le triangle ABC :
BH = 12/2 = 6
Dans le triangle rectangle ABH
Tangente de l'angle ABH = AH / BH = 9/6=3/2
Dans le triangle rectangle BMQ
Tangente de l'angle MBQ = MQ/BQ = MQ/(6-x)
MQ/(6-x) = 3/2
MQ = (3/2)(6-x) = (18-3x)/2
1.b) Prouver que l'aire A(x) du rectangle MNQP peut s'écrire A(x) = -3 [(x-3)²-9)
> Réponse trouvée
A(x) = MQ * QH
Donc : (18-3x)/2* 2x
= (36x-6x)²/2
= 36x/2 - 6x²/2
(simplification)
= 18x - 3x²
= -3x² + 18x
(facteur commun : -3x² + 3*6x
= -3 (x²-6x)
Puis : 2nde étape !
-3 [(x-3)²-9]
(identité remarquable)
= -3 [(x²-6x+9)-9]
= -3 (x²-6x)
= A(x)
2.a) Sur quel intervalle la fonction A est-elle définie ?
> Réponse trouvée :
Puisque une longueur est toujours positive, x devra forcément etre supérieur ou égal à 0. Donc x superieur ou egal 0
De plus, BC = 12 donc 2x inferieur ou egal 12. D'où x inferieur ou egal 6
Par conséquent, L'intervalle de la fonction A sera : I = [0;6]
2.b) Etudier les variations de la fonction x (x-3)² sur l'intervalle [0;6]
> Réponse trouvée : Aucune
2.c) En déduire les variations de la fonction A sur l'intervalle [0;6]
> Réponse trouvée : Aucune
3.a) Montrer que la fonction A admet un maximum. Quelle est sa valeur?
> Réponse trouvée : pas encore cherché
3.b) Calculer les dimensions du rectangle d'aire maximale.
> Réponse trouvée : Pas eu le temps de chercher non plus ...
Voila ... J'espère que vous c'est assez bien présenté ! =)
Merci pour ceux qui pourront aider !
