Maths _ spé arithmétique

[Popo]

Bonjour ,

J'ai un DM en spé à faire mais je suis coincé et si on ne réussit pas à faire une question , on ne peut pas faire la suite .

Voici le sujet :

"Les nombres dont l'écriture décimale n'utilise que le seul chiffre 1 peuvent-ils être premiers ?"
Pour tout entier naturel p>ou égal à 2 , on pose Np=1.....1 où 1 apparaît p fois .
On rappelle dès lors que Np=10^(p-1)+10^(p-2)+...+10^0

1°)Les nombres N2=11,N3=111,N4=1111 son-ils premiers ?

J'ai écrit qu'il suffisait de chercher si les nombres premiers inférieurs à racine de n (n étant N2,N3,N4) divisent n .Si aucun de ces nombres ne divisent n alors n est premier .
-11 est premier, en effet aucun des entiers premiers inférieurs à 3 ne le divise.
-111n'est pas premier car 111 est divisible par 3.
-1111 n'est pas premier car 1111 est divisible par 11.

Je voudrai avoir confirmation sur le procédé que j'ai utilisé .

2°)Prouver que Np=(10^(p-1))/(9) .Peut-on être certain que 10^(p-1) est divisible par 9?

3°)On se propose de démontrer que si p n'est pas premier alors Np n'est pas premier .
On rappelle que pour tout nombre réel x et tout entier naturel n non nul,
x^(n-1)=((x-1)(x^(n-1)+x^(n-2)+....+x+1))
a)On suppose que p est pair et on pose p=2q,où q est un entier naturel plus grand que 1.

Montrer que Np est divisible par N2=11

Merci d'avance pour votre aide

[becirj]

Bonsoir
La première question est correcte
Pour la deuxième ,le texte ne serait-il pas plutôt .
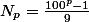
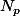
Si oui, en multipliant par 9, tu devrais arriver au résultat.

[Popo]

non ,Np=(10^(p-1))/(9) c'est 10 puissance p-1 , le tout divisé par 9 .

[yos]

Ton énoncé est faux et becirj a mis un zéro en trop.
Np=[(10^p)-1)]/(10-1) somme de termes consécutifs d'une suite géométrique.

[Popo]

mon enonce n'est pas faux ,à moins que le prof ait fait une faute de frappe

[Anonyme]

Salut !
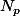
Ton prof a fait une faute de frappe alors. est plus grand que , comment pourrait-il être égal à ?

[yos]

111...1 X 9 = 999...9 = (10^n) - 1

[becirj]

Effectivement, j'ai tapé un zéro en trop . Ah! les fautes de frappe !

[Popo]

Vous avez raison , j'ai demandé à mon prof et Np=((10^p)-1)/9

[becirj]

en utilisant la deuxième question et l'indication donné.
Le nombre de termes de la somme est 2q, c'est un nombre pair et on peut regrouper les termes 2 à 2 ce qui donne :

ce qui permet de mettre 11 en facteur on obtient donc un multiple de 11.

[yos]

Ou encore
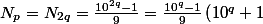pas premier.

[Popo]

Pour la 2 , il suffit de dire que 11111...1111 x 9 =999...999 =10^(p)-1 et pour la deuxieme partie de la question , je ne vois pas comment l'expliquer

Merci d'avance

[Popo]

Aidez-moi s'il vous plait

[becirj]

Je ne vois pas très bien l'intérêt de la question.
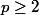
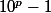
Par hypothèse donc s'écrit avec p chiffres 9 , il est bien divisible par 9.
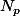
ON peut également dire que par définition est un entier.