Dm math sommes des n premiers carrés
23 messages
- Page 1 sur 2 - 1, 2
Dm math sommes des n premiers carrés
Bonjour,
J’ai ici un devoir maison de mathématique et je n’y arrive pas sur certaines questions. Je viens ici pour essayer de trouver de l’aide et des explications. merci d’avance
Voici mon énoncé
Pour tout n appartient à N on considère les sommes suivantes :
Sn= 1+2+3+...+n
Dn= 1+2²+3²+...+n²
Tn= 1+2³+3³+...+n³
1.Rappeler la propriété du cours concernant Sn
2.Montrer que T(n+1)-Tn = (n + 1)³
3.a)Montrer que (n+1)³ = n³+3n²+3n+1
On notera cette égalité En.
b)En ajoutant membre à membre les égalité En, E(n-1), E(n-2), ... , E3, E2, E1 montrer qu’on a :
T(n+1) = Tn + 3Dn + 3Sn + n + 1
4.A l’aide des questions précédentes montrer que :
1+2²+3²+...+n² = n(n+1)(2n+1)/6
Voici mes réponses :
1. Sn= n(n+1)/2
2. T(n+1)-Tn
= n^4+ 6n^3 +13n^2+ 12n+ 4/4
= n^2(n+1)^2/4 = (n+1)^3
3.a) j’ai développer
b) j’ai calculer les égalité E(n-1), E(n-2), E3, E2 et E1 mais je ne comprend pas ce que je doit faire après
4.Je n’arrive pas à montrer l’égalité
voilà j’espère que vous pourrez m’aider merci à vous.
J’ai ici un devoir maison de mathématique et je n’y arrive pas sur certaines questions. Je viens ici pour essayer de trouver de l’aide et des explications. merci d’avance
Voici mon énoncé
Pour tout n appartient à N on considère les sommes suivantes :
Sn= 1+2+3+...+n
Dn= 1+2²+3²+...+n²
Tn= 1+2³+3³+...+n³
1.Rappeler la propriété du cours concernant Sn
2.Montrer que T(n+1)-Tn = (n + 1)³
3.a)Montrer que (n+1)³ = n³+3n²+3n+1
On notera cette égalité En.
b)En ajoutant membre à membre les égalité En, E(n-1), E(n-2), ... , E3, E2, E1 montrer qu’on a :
T(n+1) = Tn + 3Dn + 3Sn + n + 1
4.A l’aide des questions précédentes montrer que :
1+2²+3²+...+n² = n(n+1)(2n+1)/6
Voici mes réponses :
1. Sn= n(n+1)/2
2. T(n+1)-Tn
= n^4+ 6n^3 +13n^2+ 12n+ 4/4
= n^2(n+1)^2/4 = (n+1)^3
3.a) j’ai développer
b) j’ai calculer les égalité E(n-1), E(n-2), E3, E2 et E1 mais je ne comprend pas ce que je doit faire après
4.Je n’arrive pas à montrer l’égalité
voilà j’espère que vous pourrez m’aider merci à vous.
Re: Dm math sommes des n premiers carrés
Bonjour
écris bien toutes tes égalités les unes sous les autres
et à la fin
tu en fais la somme membre à membre
somme de tous les membres de gauche = somme de tous les membres de droite
mais à droite, fais des sommes (je dirais) "verticales" plutôt que de tout écrire en ligne
....
écris bien toutes tes égalités les unes sous les autres
et à la fin
tu en fais la somme membre à membre
somme de tous les membres de gauche = somme de tous les membres de droite
mais à droite, fais des sommes (je dirais) "verticales" plutôt que de tout écrire en ligne
....
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Dm math sommes des n premiers carrés
Pour la question 1, j'aurais aimé voir appaaître un certain mot ... La formule que tu donnes, elle vient d'un paragraphe du cours, qui s'appelle comment ?
Question 2. Je ne sais pas d'où tu sors ces calculs, tu as un n^4 qui arrive de je ne sais où ( je devine ... mais peu importe).
En particulier, tu écris : n^4+ 6n^3 +13n^2+ 12n+ 4/4 = (n+1)^3
Si je remplace n par 1000 dans cette formule, c'est évident que c'est faux.
Cette question 2 est très facile, presque trop. Tu dois enfoncer un clou, tu as un marteau, mais tu préfères utiliser une mitrailleuse.
Question 2. Je ne sais pas d'où tu sors ces calculs, tu as un n^4 qui arrive de je ne sais où ( je devine ... mais peu importe).
En particulier, tu écris : n^4+ 6n^3 +13n^2+ 12n+ 4/4 = (n+1)^3
Si je remplace n par 1000 dans cette formule, c'est évident que c'est faux.
Cette question 2 est très facile, presque trop. Tu dois enfoncer un clou, tu as un marteau, mais tu préfères utiliser une mitrailleuse.
Re: Dm math sommes des n premiers carrés
merci de vos réponses
alors pour la question 1 j’ai trouver la formule dans mon cours qui s’appelle sommes des n premiers entiers naturels non nuls.
pour la 2 j’ai trouver que
T(n+1)=(n+1)^2((n+1)+1)^2/4
= n^4 + 6n^3 + 13n^2 + 12n + 4/4
c’est de là où j’ai trouver le n^4
et oui je me suis tromper j’ai oublier de soustraire le Tn
donc cela fait
n^4 + 6n^3 + 13n^2 + 12n + 4/4 - n^2(n+1)^2/4
= (n+1)^3
pour la 3b) j’ai fait la sommes des membres à la verticales mais je n’arrive pas à retrouver l’égalité
T(n+1)= Tn + 3Dn + 3Sn + n + 1
je n’arrive pas à transformer mon résultat afin de trouver ça.
alors pour la question 1 j’ai trouver la formule dans mon cours qui s’appelle sommes des n premiers entiers naturels non nuls.
pour la 2 j’ai trouver que
T(n+1)=(n+1)^2((n+1)+1)^2/4
= n^4 + 6n^3 + 13n^2 + 12n + 4/4
c’est de là où j’ai trouver le n^4
et oui je me suis tromper j’ai oublier de soustraire le Tn
donc cela fait
n^4 + 6n^3 + 13n^2 + 12n + 4/4 - n^2(n+1)^2/4
= (n+1)^3
pour la 3b) j’ai fait la sommes des membres à la verticales mais je n’arrive pas à retrouver l’égalité
T(n+1)= Tn + 3Dn + 3Sn + n + 1
je n’arrive pas à transformer mon résultat afin de trouver ça.
Re: Dm math sommes des n premiers carrés
bonjour,
soit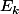 l'égalité
l'égalité ^3=k^3+3k^2+3k+1)
on somme les égalités) de k=0 jusqu'à n, soit n+1 égalités.
de k=0 jusqu'à n, soit n+1 égalités.
Qu'est ce que l'on obtient ?
soit
on somme les égalités
Qu'est ce que l'on obtient ?
Re: Dm math sommes des n premiers carrés
mathelot a écrit:bonjour,
soitl'égalité
on somme les égalitésde k=0 jusqu'à n, soit n+1 égalités.
Qu'est ce que l'on obtient ?
on obtient:
(on a tout additionné mais .. en colonnes)
Re: Dm math sommes des n premiers carrés
Bonjour,
mimiiii14: tu as eu des réponses sur https://www.ilemaths.net/sujet-dm-math-sommes-des-n-premiers-carres-862021.html après de nombreux échanges.
Et maintenant- tu reviens ici; sympa pour les aidants
mimiiii14: tu as eu des réponses sur https://www.ilemaths.net/sujet-dm-math-sommes-des-n-premiers-carres-862021.html après de nombreux échanges.
Et maintenant- tu reviens ici; sympa pour les aidants
Re: Dm math sommes des n premiers carrés
L'addition en colonnes (x,y,z,a,b,c,d,e,f des réels):
x=a+b
y=c+d
z=e+f
x+y+z=(a+b)+(c+d)+(e+f)= (a+c+e)+(b+d+f)
comprends-tu cette addition en colonnes ? elle résulte de la commutativité et de l'associativité de l'addition
x=a+b
y=c+d
z=e+f
x+y+z=(a+b)+(c+d)+(e+f)= (a+c+e)+(b+d+f)
comprends-tu cette addition en colonnes ? elle résulte de la commutativité et de l'associativité de l'addition
Modifié en dernier par mathelot le 10 Jan 2021, 21:13, modifié 1 fois.
Re: Dm math sommes des n premiers carrés
Bonjour
oui d’accord merci j’ai compris pour l’addition en colonnes
il faut que j’additionne verticalement les égalités que j’ai trouvé pour
En, En-1, En-2, E3, E2 et E1 ?
oui d’accord merci j’ai compris pour l’addition en colonnes
il faut que j’additionne verticalement les égalités que j’ai trouvé pour
En, En-1, En-2, E3, E2 et E1 ?
Re: Dm math sommes des n premiers carrés
on additionne aussi l'égalité 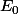 qui vaut
qui vaut 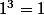 , soit en tout n+1 égalités
, soit en tout n+1 égalités
Re: Dm math sommes des n premiers carrés
Pisigma a écrit:Bonjour,
mimiiii14: tu as eu des réponses sur https://www.ilemaths.net/sujet-dm-math-sommes-des-n-premiers-carres-862021.html après de nombreux échanges.
Et maintenant- tu reviens ici; sympa pour les aidants
Bonjour
j’ai chercher des réponses sur ces deux sites afin d’avoir différentes façon de résolutions et différents raisonnements. Je ne voulais pas manquer de respect aux aidant.
Re: Dm math sommes des n premiers carrés
D’accord il faut que j’additionne toutes ces égalités merci.
Re: Dm math sommes des n premiers carrés
mathelot a écrit:Est ce que tu connais le signe(sigma pour somme)
?
?
Re: Dm math sommes des n premiers carrés
oui je connais ce signe mais je ne comprend pas trop comment est ce qu’il faut l’utiliser.
Re: Dm math sommes des n premiers carrés
d’accord je vois j’ai compris et c’est avec ça que je dois montrer l’égalité à la question 4 ?
Re: Dm math sommes des n premiers carrés
non, c'était plutôt pour la question (3).
Pour la (4), on connait-T(n)) et
et  , ce qui permet de calculer
, ce qui permet de calculer 
Pour la (4), on connait
Re: Dm math sommes des n premiers carrés
ah d’accord mais dans la question 3 je n’arrive pas faire la somme dés égalité et à trouver le même résultats.
Re: Dm math sommes des n premiers carrés
La ligne ) s'écrit :
s'écrit : ^3=k^3+3k^2+3k+1)
On somme (n+1) égalités en faisant varier k de 0 à n:
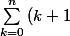^3 = \sum_{k=0}^n k^3+3 \sum_{k=0}^n \, k^2 +3\sum_{k=0}^n \, k +\sum_{k=0}^n 1)
=T(n) + 3 D_n +3 S_n + (n+1))
On somme (n+1) égalités en faisant varier k de 0 à n:
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
