Les n premiers entiers, carrés et cubes
18 messages
- Page 1 sur 1
Les n premiers entiers, carrés et cubes
Bonsoir a toues et à tous, j'ai un petit souci sur un exercice et je 'arrive pas a le résoudre
1. Déterminer un polynôme f(x) du second degré tel que :
Pour tout x appartenant à R f(x+1) - f(x) = x
J'ai choisi f(x) = ax²+bx+c
Donc la je bloque à 2ax+a+b=x
Et je ne vois pas ce que je doit faire ( même si je me doute que ce n'es pas très compliqué, je manque d'inspiration ^^)
En déduire la somme S1= 1+2+3+...+n
2. Déterminer un polynôme g(x) du troisième degré tel que :
Pour tout x appartenant à R g(x+1) - g(x) = x²
en choisissant au départ g(x)=ax^3+bx²+cx+d
Je me retouve bloqué au même endroit, c'est a dire,
3ax²+3ax+a+2bx+b+c = x²
En déduire la somme S2= 1²+2²+3²+...+n²
3. idem que les deux autres avec un polynôme du 4 ème degré pour la somme des n premiers cube
je pense que c'est le même raisonnement qu'avec le premier de toute façon donc, cce ne sera pas la peine de m'expliquer
Merci d'avance ^^
1. Déterminer un polynôme f(x) du second degré tel que :
Pour tout x appartenant à R f(x+1) - f(x) = x
J'ai choisi f(x) = ax²+bx+c
Donc la je bloque à 2ax+a+b=x
Et je ne vois pas ce que je doit faire ( même si je me doute que ce n'es pas très compliqué, je manque d'inspiration ^^)
En déduire la somme S1= 1+2+3+...+n
2. Déterminer un polynôme g(x) du troisième degré tel que :
Pour tout x appartenant à R g(x+1) - g(x) = x²
en choisissant au départ g(x)=ax^3+bx²+cx+d
Je me retouve bloqué au même endroit, c'est a dire,
3ax²+3ax+a+2bx+b+c = x²
En déduire la somme S2= 1²+2²+3²+...+n²
3. idem que les deux autres avec un polynôme du 4 ème degré pour la somme des n premiers cube
je pense que c'est le même raisonnement qu'avec le premier de toute façon donc, cce ne sera pas la peine de m'expliquer
Merci d'avance ^^
Bon allez je t'aide pour la 1)
Pour le polynôme t'y était presque, après avoir trouvé l'équation 2ax+a+b=0 il fallait simplement résoudre le système
2a = 1
a + b = 0
Ceci implique a= 1/2 et b = -1/2
Finalement ton polynôme a cette tête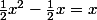
Ainsi-f(x)=x \ \Longleftrightarrow \ \frac{1}{2}(x+1)^2-\frac{1}{2}(x+1) - (\frac{1}{2}x^2-\frac{1}{2}x)=x \\ \Longleftrightarrow \frac{1}{2}[ \ (x+1)^2 -x^2 - (x+1) +x \ ] =x \ \ \ (1))
Je te rappelle également que
Du coup tu passe a la somme dans l'équation (1)
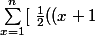^2 -x^2 - (x+1) +x) \ ]=\sum_{x=1}^n x \\ \Longleftrightarrow \frac{1}{2}(\sum_{x=1}^n(x+1)^2 -\sum_{x=1}^nx^2 - \sum_{x=1}^n (x+1) +\sum_{x=1}^n x) =\sum_{x=1}^n x \ \ \ (2))
La il faut remarquer que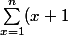^2 -\sum_{x=1}^nx^2) est ce qu'on appelle une somme télescopique c'est à dire que les deux sommes s'annulent partiellement entre elles de façon a ce qu'il ne subsiste que deux termes :
est ce qu'on appelle une somme télescopique c'est à dire que les deux sommes s'annulent partiellement entre elles de façon a ce qu'il ne subsiste que deux termes :
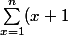^2 -\sum_{x=1}^nx^2 \ = \ ( 2^2 + 3^2+...n^2+\LARGE(n+1)^2\normalsize)- (\LARGE 1^2 \normalsize + 2^2+...+n^2) \\ = (n+1)^2 - 1)
Par le même raisonnement on a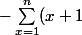 \ + \ \sum_{x=1}^n x = -(n+1) +1)
Après ces petits calculs intermédiaires revenons a notre équation (2) qui nous donne donc :
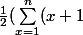^2 -\sum_{x=1}^nx^2 - \sum_{x=1}^n (x+1) +\sum_{x=1}^n x) =\sum_{x=1}^n x \\ \Longleftrightarrow \ \frac{1}{2}((n+1)^2 -1 -(n+1) +1) = \sum_{x=1}^n x \\ \Longleftrightarrow \ \frac{1}{2}((n+1)^2 -(n+1)) = \sum_{x=1}^n x \\ \Longleftrightarrow \ \frac{1}{2}((n+1)(n+1-1)) = \sum_{x=1}^n x \ (factorisation) \\ \Longleftrightarrow \ \sum_{x=1}^n x =\frac{n(n+1)}{2})
En conclusion}{2})
J'espère t'avoir éclairé et maintenant a toi de faire les autres questions :we:
Pour le polynôme t'y était presque, après avoir trouvé l'équation 2ax+a+b=0 il fallait simplement résoudre le système
2a = 1
a + b = 0
Ceci implique a= 1/2 et b = -1/2
Finalement ton polynôme a cette tête
Ainsi
Je te rappelle également que
Du coup tu passe a la somme dans l'équation (1)
La il faut remarquer que
Par le même raisonnement on a
Après ces petits calculs intermédiaires revenons a notre équation (2) qui nous donne donc :
En conclusion
J'espère t'avoir éclairé et maintenant a toi de faire les autres questions :we:
dsl exarkun mais j'ai rien compris avec les sigma, les somme téléscopique ou je ne sais pas trop quoi ^^
Je suis en seulement en première :triste:
j'ai compris tout de même que le polynôme du second degré vérifiant l'équation est 1/2x²-1/2x
Après notre prof nous a conseillé d'écrire :
f(2)-f(1)=1
f(3)-f(2)=2
f(4)-f(3)=3
. .
. .
. .
f(n+1)-f(n)=n
Et de tout ajouter membre à membre
et je trouve -f(1)+f(4)+f(n+1)-f(n)=6+n
Et le, reblocage :mur:
merci de votre aide
Je suis en seulement en première :triste:
j'ai compris tout de même que le polynôme du second degré vérifiant l'équation est 1/2x²-1/2x
Après notre prof nous a conseillé d'écrire :
f(2)-f(1)=1
f(3)-f(2)=2
f(4)-f(3)=3
. .
. .
. .
f(n+1)-f(n)=n
Et de tout ajouter membre à membre
et je trouve -f(1)+f(4)+f(n+1)-f(n)=6+n
Et le, reblocage :mur:
merci de votre aide
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
