j'ignore si je doit faire un sujet pour un ex mais dans le doute j'en fait un )
RE !! bon j'ai passé l'exercice 1 et une partit du 3 mais j'ai encore un problème (un peu plus important qu'une simple hésitation cette fois)
donc comme je l'est dit sur mon premier sujet ce DM est sur un sujet jamais vu en classe et si j'ai pu m'appuyer sur votre aide et sur mais connaissance de 3em pour l'ex 1 pour l'ex 2 c'est un peu plus compliqué
donc l'énoncé reste le même : factorisé les expressions suivantes
mais cette fois les expression se présente comme sa :
A=49x² - 9
B=100x²+100x+25
C=25x² - 90x+81
D=25x² - 70x+49
E=16x² - 49
F=3x²+2;)3x+1
donc je sais que pour factoriser il faut obligatoirement cette forme : .....*......+/-......*....... (*=signe fois)
et après recherche (merci internet) pour modifier une expression et pouvoir la factoriser on peut faire
*1
par ex : 49*x² - 9*1 et la en théorie on peut factoriser mais la grande question c'est qu'il n'y a pas de facteur commun et que pour l'expression B D F et C la technique ne marche même pas car il y a deux signe -/+
donc cette fois si je sèche totalement quelqu'un pourrai t'il m'expliquer ou me rediriger vers un lien qui expliquerai comment faire ???
DM math seconde (2)
9 messages
- Page 1 sur 1
il s'agit d'utiliser les identités remarquables
^2)
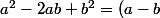^2)
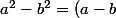(a+b))
prenons la (c) à titre d'exemple

i) on repère les deux carrés
ii) on vérifie la présence du double produit : 2ab
iii) on vérifiee si l'on a: +2ab ou -2ab
iv) dans l'affirmative, on factorise
C=25x^2 - 90x+81
produit simple:
produit double:
donc
C=25x^2 - 90x+81
= (5x-9)^2
prenons la (c) à titre d'exemple
i) on repère les deux carrés
ii) on vérifie la présence du double produit : 2ab
iii) on vérifiee si l'on a: +2ab ou -2ab
iv) dans l'affirmative, on factorise
C=25x^2 - 90x+81
produit simple:
produit double:
donc
C=25x^2 - 90x+81
= (5x-9)^2
eljojoloco a écrit:j'ignore si je doit faire un sujet pour un ex mais dans le doute j'en fait un )
RE !! bon j'ai passé l'exercice 1 et une partit du 3 mais j'ai encore un problème (un peu plus important qu'une simple hésitation cette fois)
donc comme je l'est dit sur mon premier sujet ce DM est sur un sujet jamais vu en classe et si j'ai pu m'appuyer sur votre aide et sur mais connaissance de 3em pour l'ex 1 pour l'ex 2 c'est un peu plus compliqué
donc l'énoncé reste le même : factorisé les expressions suivantes
mais cette fois les expression se présente comme sa :
A=49x² - 9
B=100x²+100x+25
C=25x² - 90x+81
D=25x² - 70x+49
E=16x² - 49
F=3x²+2;)3x+1
donc je sais que pour factoriser il faut obligatoirement cette forme : .....*......+/-......*....... (*=signe fois)
et après recherche (merci internet) pour modifier une expression et pouvoir la factoriser on peut faire
*1
par ex : 49*x² - 9*1 et la en théorie on peut factoriser mais la grande question c'est qu'il n'y a pas de facteur commun et que pour l'expression B D F et C la technique ne marche même pas car il y a deux signe -/+
donc cette fois si je sèche totalement quelqu'un pourrai t'il m'expliquer ou me rediriger vers un lien qui expliquerai comment faire ???
Bonjour,
Utilise :
a²-b²=(...)(...)
(a+b)²=...+...+...
coucou (désolé pour le double post)
alors j'ai respectivement trouvés :
A=49x² - 9 =(7x+3) (7x-3)
B=100x²+100x+25 =(10x+5)²
C=25x² - 90x+81 =(5x-9)²
D=25x² - 70x+49 =(5x-7)²
E=16x² - 49 =(4x+7) (4x-7)
F=3x²+2;)3x+1 =(;)3x+1)²
alors première question ces résultat sont t'il juste
et deuxième je sais qu'il suffit de faire la de A et B pour arriver a la forme factorisé mais existe t'il une présentation/une phrase a écrire pour prouver le calcule ou il suffit juste de placé le signe;) devant les nombre ? ( ex : E=;) 16x² - ;) 49 =(4x+7) (4x-7)
de A et B pour arriver a la forme factorisé mais existe t'il une présentation/une phrase a écrire pour prouver le calcule ou il suffit juste de placé le signe;) devant les nombre ? ( ex : E=;) 16x² - ;) 49 =(4x+7) (4x-7)
et C=;) 25x² - 90x+;) 81 =(5x-9)² ) ou faut il une présentation particulière ??
alors j'ai respectivement trouvés :
A=49x² - 9 =(7x+3) (7x-3)
B=100x²+100x+25 =(10x+5)²
C=25x² - 90x+81 =(5x-9)²
D=25x² - 70x+49 =(5x-7)²
E=16x² - 49 =(4x+7) (4x-7)
F=3x²+2;)3x+1 =(;)3x+1)²
alors première question ces résultat sont t'il juste
et deuxième je sais qu'il suffit de faire la
et C=;) 25x² - 90x+;) 81 =(5x-9)² ) ou faut il une présentation particulière ??
Salut,
Ces résultats sont justes.
Pour la justification du calcul, ne procède surtout pas comme cela.
16x² - 49 = (4x+7)(4x-7), c'est l'identité remarquable qui te permet de le dire, mais
 16x² -
16x² -  49 n'est pas égal à (4x+7)(4x-7).
49 n'est pas égal à (4x+7)(4x-7).
Afin de justifier tes résultats, contente toi de donner à chaque fois l'identité remarquable que utilises.
Par exemple, voici ce que je mettrais sur la copie pour le A :
A = 49x² - 9
Je remarque la présence de deux carrés, mais pas d'un double produit.
Je factorise donc en utilisant l'identité remarquable a² - b² = (a+b)(a-b).
Ce qui nous donne :
A = (7x+3)(7x-3)
Bien sûr, ce n'est probablement pas la meilleure façon de justifier, personnellement je suis plus dans la rédaction qu'autre chose, fais comme tu le sens, mais évite d'effectuer des opérations sur ton expression de base et de prétendre qu'elle reste identique... 16x² - 49 n'est pas égal à 16x² -
16x² -  49.
49.
Ces résultats sont justes.
Pour la justification du calcul, ne procède surtout pas comme cela.
16x² - 49 = (4x+7)(4x-7), c'est l'identité remarquable qui te permet de le dire, mais
Afin de justifier tes résultats, contente toi de donner à chaque fois l'identité remarquable que utilises.
Par exemple, voici ce que je mettrais sur la copie pour le A :
A = 49x² - 9
Je remarque la présence de deux carrés, mais pas d'un double produit.
Je factorise donc en utilisant l'identité remarquable a² - b² = (a+b)(a-b).
Ce qui nous donne :
A = (7x+3)(7x-3)
Bien sûr, ce n'est probablement pas la meilleure façon de justifier, personnellement je suis plus dans la rédaction qu'autre chose, fais comme tu le sens, mais évite d'effectuer des opérations sur ton expression de base et de prétendre qu'elle reste identique... 16x² - 49 n'est pas égal à
Grimmys a écrit:Salut,
Ces résultats sont justes.
Pour la justification du calcul, ne procède surtout pas comme cela.
16x² - 49 = (4x+7)(4x-7), c'est l'identité remarquable qui te permet de le dire, mais16x² -
49 n'est pas égal à (4x+7)(4x-7).
Afin de justifier tes résultats, contente toi de donner à chaque fois l'identité remarquable que utilises.
Par exemple, voici ce que je mettrais sur la copie pour le A :
A = 49x² - 9
Je remarque la présence de deux carrés, mais pas d'un double produit.
Je factorise donc en utilisant l'identité remarquable a² - b² = (a+b)(a-b).
Ce qui nous donne :
A = (7x+3)(7x-3)
Bien sûr, ce n'est probablement pas la meilleure façon de justifier, personnellement je suis plus dans la rédaction qu'autre chose, fais comme tu le sens, mais évite d'effectuer des opérations sur ton expression de base et de prétendre qu'elle reste identique... 16x² - 49 n'est pas égal à16x² -
49.
merci beaucoup !
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
