Limites, tan(x)...
14 messages
- Page 1 sur 1
Limites, tan(x)...
Bonjour à vous.
Je viens vous demander de l'aide pour un petit excercice tout bête.
Demain, j'ai un DS de maths sur les limites et tout ce qui s'y réfère (terminale S) et j'aimerais que vous me disiez, en dehors du cours, les trucs bons à savoir et qui peuvent m'aider (genre sinus, cosinus, etc).
D'ailleurs, résoudre lim(tanx) quand x=>+l'inf, vous savez-faire?
J'avais pensé à faire tanx=sinx/cosx.
Merci
Je viens vous demander de l'aide pour un petit excercice tout bête.
Demain, j'ai un DS de maths sur les limites et tout ce qui s'y réfère (terminale S) et j'aimerais que vous me disiez, en dehors du cours, les trucs bons à savoir et qui peuvent m'aider (genre sinus, cosinus, etc).
D'ailleurs, résoudre lim(tanx) quand x=>+l'inf, vous savez-faire?
J'avais pensé à faire tanx=sinx/cosx.
Merci
Nightmare a écrit:Salut,
on ne "résout" pas une limite, on la calcule, quand c'est possible. En l'occurrence ici, si tu traces le graphe de la fonction tangente (ou demande à ta calculette/logiciel préféré de le faire), elle te semble se comporter comment cette fonction pour des x très grands?
J'arrive même pas à la tracer sur ma calculette
C'est une casop graph35+
Je vais dans "graph", je tape Y1=TanX et je vois une sorte de droite jusqu'à environ -1 d'abscisse puis plus rien...
Mais à mon avis, on peut la résoudre sans, on ne peut résoudre une limite par interprétation graphique, sauf si demandé.
D'ailleurs, quand je trace cosX ça me met une droite parallèle à l'axe des abscisses...
merci de me répondre
Nightmare a écrit:As-tu vérifié que ta calculette était en radian?
Sinon, ma remarque concernant l'utilisation du mot "résoudre" n'a pas l'air de t'avoir intéressée :lol3:
Si, elle m' intéressé, cependant, je le sais, c'est juste que je ne suis pas hyper concentré. Je te garanti que dans le devoir je ne le ferai pas
Et donc, pour le CALCUL ( :id: ) de la limite? (sans la représentation).
(Je ne sais même plus comment remettre en radian lol)
colro51 a écrit:Demain, j'ai un DS de maths sur les limites et tout ce qui s'y réfère (terminale S) et j'aimerais que vous me disiez, en dehors du cours, les trucs bons à savoir et qui peuvent m'aider
demande s'il y a des frites à la cantine...
non , je plaisante
les trucs bons à savoir:
1) les racines : la quantitée conjuguée
2) la meilleure approximation affine
3) le théorème du divin marquis
(le Marquis de l'Hospital, pas l'autre :we: )
4) interpréter les quotients comme la recherche de nombre dérivé
5) encadrer par deux gendarmes si ça oscille trop
6) les encadrement se démontrent avec une fonction de travail
strictement croissante
7) pour la continuité, un raccord avec
lim à droite et lim à gauche
mathelot a écrit:demande s'il y a des frites à la cantine...
non , je plaisante
les trucs bons à savoir:
1) les racines : la quantitée conjuguée
2) la meilleure approximation affine
3) le théorème du divin marquis
(le Marquis de l'Hospital, pas l'autre :we: )
4) interpréter les quotients comme la recherche de nombre dérivé
5) encadrer par deux gendarmes si ça oscille tropau voisinage de l'infini
6) les encadrement se démontrent avec une fonction de travail
strictement croissante
7) pour la continuité, un raccord avec
lim à droite et lim à gauche
Lol, c'est un DS sur la continuité (très peu) et sur les LIMITES, mais pas touche aux dérivées et tout (d'ailleurs je connais pas "quantités conjuguées" pour les racines, qu'est-ce?).
Sinon, oui, gendarmes, limites droite/gauche pour la continuité etc...
T'as une solution pour mon pb de tangente ?
merci de me rep.
1)
quantité conjuguée
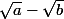 et
et 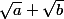
sont conjuguées, leur produit ne comporte plus de racine carrée
(un peu comme 2 inverses, si tu veux)
2° la meilleure approximation affine
c'est une application affine

qui est censée bien approcher f(x) qd x est voisin de
alors)
 est la différentielle de f en
est la différentielle de f en 
elle indique comment f transforme les accroissements
c'est donc \Delta_x)
en 1ère approximation, il ya toujours de la linéarité
entre l'accroissement de la variable et l'accroissement de l'image
et l'accroissement de l'image )
quantité conjuguée
sont conjuguées, leur produit ne comporte plus de racine carrée
(un peu comme 2 inverses, si tu veux)
2° la meilleure approximation affine
c'est une application affine
qui est censée bien approcher f(x) qd x est voisin de
alors
elle indique comment f transforme les accroissements
c'est donc
en 1ère approximation, il ya toujours de la linéarité
entre l'accroissement de la variable
mathelot a écrit:1)
quantité conjuguéeet
sont conjuguées, leur produit ne comporte plus de racine carrée
(un peu comme 2 inverses, si tu veux)
2° la meilleure approximation affine
c'est une application affine
qui est censée bien approcher f(x) qd x est voisin de
alorsest la différentielle de f en
elle indique comment f transforme les accroissements
c'est donc
en 1ère approximation, il ya toujours de la linéarité
entre l'accroissement de la variableet l'accroissement de l'image
Effectivement, j'ai vu le truc des racines. On les utilise uniquement quand on aboutit à une forme indeterminée de forme "0/0" nous, n'est-ce pas?
Par contre, je ne crois pas avoir besoin de l'approximation affine, c'est plutôt du programme des dérivées, il me semble.
colro51 a écrit:Effectivement, j'ai vu le truc des racines. On les utilise uniquement quand on aboutit à une forme indeterminée de forme "0/0" nous, n'est-ce pas?
Par contre, je ne crois pas avoir besoin de l'approximation affine, c'est plutôt du programme des dérivées, il me semble.
Et pour les formes inteterminées, c'est quoi les méthodes?
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
