Limite en l'infini d'une fraction

[novicemaths]

Bonsoir

Pourriez-vous me dire quel méthode à employer pour déterminer la limité en - infinie de la fonction ci-dessous.



J'ai pensé au terme du plus au degré et à la factorisation, je ne vois pas comment attaquer le dénominateur.

A bientôt

[pascal16]

la méthode de base, c'est bien de mettre x^5 en facteur au dénominateur, on peut, persque sans plus de justification dire que c'est 0.

une astuce ici est de "sortir" x du premier facteur du dénominateur
on traite alors x*le second terme du dénominateur (exposant 4 tous les deux), on dit simplement que ça converge vers une constante. Et, même en justifiant, les calculs sont moins longs

la limite est alors la même que (constante)/(2x-3)

[novicemaths]

Re bonsoir



Est-ce que la factorisation est correct?

A bientôt

[pascal16]

elle est juste, mais elle ne permet pas de conclure. Il faudrait développer le dénominateur avant.


mais :
(4x²-3x)(3*x^3-4x²) = x (4x-3)(3*x^3-4x²) = (4x-3)(3*x^4-4x^3) = (4x-3)*x^4*(3-4/x)

et tu peux simplifier le x^4 avec celui du numérateur

[abdelmalek.2008]

Bonsoir

Pourriez-vous me dire quel méthode à employer pour déterminer la limité en - infinie de la fonction ci-dessous.



J'ai pensé au terme du plus au degré et à la factorisation, je ne vois pas comment attaquer le dénominateur.

A bientôt

---------------------

[hdci]

Bonsoir,

Re bonsoir



Est-ce que la factorisation est correct?

La factorisation du dénominateur est incorrecte : en effet, la factorisation se fait sur une somme pas sur un produit : quand on a , ce n'est pas égal (en général) à !

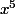
Pour avoir en facteur, il faut factoriser dans le premier facteur et dans le second :