Limite et continuité

[h24]

Soit f:R+ → R+ une fonction continue. On suppose
que la fonction h(x)=f(x)/x admet une limite
finie l< 1 en + l'infinie . Démontrer que : qu'il existe e tell que f(e)=e
J'ai pas su comment utilisé TVI dans ce cas
Merci pour votre aide!

[Landstockman]

Trouver un tel e c'est comme trouver e qui vérifie
Donc tu appliques le TVI à la fonction qui a associe
Que se passe-t-il en 0 et en l'infini ?

[Landstockman]

(j'ai supposé e différent de 0, à toi de voir ce qu'il se passe si e=0)

[Landstockman]

Et petite faute de frappe dans mon premier message : la fonction qui à associe

[h24]

mais on a l inferieur strictement a 1 a quoi ca vas servire de prendre l'autre equation

[Landstockman]

Tu vas appliquer le TVI à définie sur .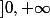
En , combien vaut g ? et en l'infini ? (attention aux sous cas).
Peut-on en déduire par le TVI que g vaut 1 à un certain endroit ? Est-ce que ça conclut ?

[Ben314]

Salut,
Perso, j'aurais plutôt étudié g(x)=f(x)-x.
Sur le principe, ça change "pas des masses" la donne vu qu'évidement, pour x->oo, j'aurais écrit que , mais justement, ça évite de s'emmer... à étudier différents cas de figure pour voir ce que donne f(x)/x lorsque x tend vers 0+ (là, g(0)=f(0)-0 qui est positif ou nul epicétout)

[Landstockman]

Ah oui c'est vrai que c'est mieux @Ben314

[h24]

mon probleme c'est que je sait pas utiliser tvi dans l'infinie

[Landstockman]

Tu as étudié la fonction de Ben314 avec un tableau de variation ?