Limite, avec puissance n.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
loxaxs
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Nov 2013, 22:39
-
 par loxaxs » 07 Nov 2013, 18:06
par loxaxs » 07 Nov 2013, 18:06
Bonjour,
Je partage cette correction avec tout le monde, puisque je cherchais la solution hier soir.
Nous savons que quand n tend vers l'infini positif, si q > 1, q^n tend vers l'infini positif.
Nous cherchons la limite (quand n tend vers l'infini positif), de l'expression:

Solution :


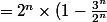)
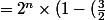^{n}))

car 2 > 1
^{n} = +\infty)
car 3/2 > 1
or le produit d'une expression qui tend vers l'infini positif (2^n) par une expression qui tend vers l'infini négatif (1-(3/2)^n) tend vers l'infini négatif.
D'ou :
^{n}) = -\infty)
Ce qui équivaux à :
 = -\infty)
----
Et voila.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 07 Nov 2013, 18:09
par Carpate » 07 Nov 2013, 18:09
loxaxs a écrit:Bonjour,
Je partage cette correction avec tout le monde, puisque je cherchais la solution hier soir.
Et voila.
Y a-t-il une question ?
Variante :
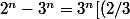^n-1])
^n \rightarrow 0)
^n-1] \rightarrow -1)

-
loxaxs
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Nov 2013, 22:39
-
 par loxaxs » 07 Nov 2013, 18:11
par loxaxs » 07 Nov 2013, 18:11
* Non, il n'y a pas de question, il n'y a là que des réponses, pour ceux que ça intéresses.
* Variante : Bien-vu, ma professeur de mathématique l'avait en-effet mentionnée au passage.
Voila.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
