Intégrales !

[maxence6]

Bonjour,

soit une fonction f(x) :





f(x) = x mais on va gardé la forme non simplifié pour l'instant, ensuite


(j'écris le resultat finale, sinon j'ai pas fini si je détaille le calcul )
Donc le résultat est de environ 0.58

maintenant on prend une autre fonction, bien quel soit égale à la précédente !
(vous suivez ? :we: )


Donc je fais intégrales de la fonction g(x) et tout et comme vous pouvez le constater en traçant sa courbe représentative ou en calculant l'intégrale on trouve

Donc naturellement on peut en conclure que f(x)=g(x) mais F(x) n'est pas égale a G(x), Pourquoi ?!?

[Billball]

f(x) vaut pas x chez moi ! (ou alors je suis a coté de la plaque)

[Skullkid]

Ton calcul de primitive est faux : on n'obtient pas les primitives d'un produit en faisant le produit des primitives. Et, contrairement à ce qui se passe pour la dérivation, il n'existe pas de formule explicite pour calculer les primitives d'un produit.

D'autre part, l'intégrale d'une fonction est un nombre, et par conséquent n'a pas d'unité. L'aire sous la courbe d'une fonction s'exprime en u.a. mais pas l'intégrale de cette fonction.

[maxence6]

on n'obtient pas les primitives d'un produit en faisant le produit des primitives.

Alors comment fait-on ?

[Sylviel]

Si tu lis la ligne suivante de la réponse tu verras qu'il n'y a pas de méthode générale, ce qui s'en approche le plus c'est l'intégration par parties. Et pour mémoire la dérivée d'un produit n'est pas le produit des dérivées...

[maxence6]

A ok, j'ai jamais entendu parler d'intégration par parti :cry:

[benekire2]

pas besoin d'IPP ! As tu seulement songer a développer ta fonction ?

[maxence6]

Oui, j'y est pensé, f(x) = x comme je l'ai dit juste avant mais je voulais juste voir, si entre deux fonctions égales, écrite de différentes façon on retombé bien sur nos pattes !

[benekire2]

Oui parfaitement , f(x)=x et ça je te laisse l'intégrer.

x est toujours une écriture de f ? Oui, donc c'est pareil que si tu intégrais x²-x(x-1)

[maxence6]

Oui je sais mais justement je n'y arrive pas, comment "primitiver" f(x) sous sa forme ?

[Billball]

bah développe ca et primitive

[maxence6]

lol Oui je veut bien mais justement le but de pas le développé c'est de voir qu'on retrouve le même résultat entre f(x) et g(x) ! :+++:

[anima]

lol Oui je veut bien mais justement le but de pas le développé c'est de voir qu'on retrouve le même résultat entre f(x) et g(x) ! :+++:

Je ne sais pas si ton énoncé cherche a te montrer que ou si . Tu peux tenter la 2e approche, et calculer en développant. Tu trouveras que .

Si tu veux vraiment intégrer directement, une intégration par parties est nécessaire. Poses et .

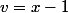
[maxence6]

Ok ok Merci !