Integrale de wallis
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 12:38
par anais39600 » 01 Nov 2009, 12:38
bonjour, si vous pouvez m'aider sa serait gentil
second ennoncé plus bas
voila l'enoncer J= integrale de 0 à 2 de racine carré (4-x² dx et x=2sint
donc j'ai x=0 et t=0
x=2 et t=pi/2 dx= 2 cos t dt
donc 4-x²= 4(1-sin²t)=4cos²t
racine 4-X²= 2 cost
soit J= integrale entre 0 et pi/2 2cost*2costdt= integrale 4 cost²
ensuite je ne vois pas commen trouver la primitive merci de m'aider

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 12:43
par Ericovitchi » 01 Nov 2009, 12:43
Oui c'est bien, tu en es à

Et bien il suffit d'appliquer la formule

-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 12:49
par anais39600 » 01 Nov 2009, 12:49
Ericovitchi a écrit:Oui c'est bien, tu en es à

Et bien il suffit d'appliquer la formule

ok mais apres je fait quoi car la je voit vraiment pas

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 13:00
par Ericovitchi » 01 Nov 2009, 13:00
1/2 s'intègre facilement (la primitive est t/2)
1/2 Cos 2t s'intègre facilement aussi (primitive 1/4 sin 2t )
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 13:00
par anais39600 » 01 Nov 2009, 13:00
la primitive de 1+cos²t/2 serait [1/2t+1/6 cos^3t]
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 13:01
par anais39600 » 01 Nov 2009, 13:01
Ericovitchi a écrit:1/2 s'intègre facilement (la primitive est t/2)
1/2 Cos 2t s'intègre facilement aussi (primitive 1/4 sin 2t )
merci jai fait une erreur j'ai garder le carré merci beaucoup
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 13:08
par anais39600 » 01 Nov 2009, 13:08
anais39600 a écrit:merci jai fait une erreur j'ai garder le carré merci beaucoup
j'ai trouver pi comme resultat final
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 14:38
par anais39600 » 01 Nov 2009, 14:38

Je doit calculer J0 ssoit pour moi Pi/2 et J1 soit 1
je doit montrer que

J'ai
x*coxxdx)
en integrant par parti j'ai u= cos^(n-1) u'= n-1cos^n-2
v= sinx v'= cos x
j'ai donc
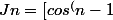*sinx]-\bigint_{0}^{Pi/2} (n-1)cos^(n-2)sinxdx)
et je m'en sort plus meme si je change les menbre de l'integration si on peu m'aider

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 14:54
par Ericovitchi » 01 Nov 2009, 14:54
u= cos^(n-1) u'= n-1cos^n-2
non quand tu dérives cos^(n-1)x ça fait
-(n-1)
sin^(n-2)x
Sinon oui tu es bien parti, il faut faire une seconde intégration par partie
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 15:49
par anais39600 » 01 Nov 2009, 15:49
Ericovitchi a écrit:non quand tu dérives cos^(n-1)x ça fait -(n-1)sin^(n-2)x
Sinon oui tu es bien parti, il faut faire une seconde intégration par partie
ok mais j'ai sa est je voit pas comment retrouver
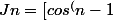sinx]+[(n-1)sin^(n-2)cosx]-\bigint_{0}^{Pi/2}(n-1)(n-2)cos^(n-3)cosx)
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 16:30
par anais39600 » 01 Nov 2009, 16:30
si on pouvait m'aider se serait sympa

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 16:39
par Ericovitchi » 01 Nov 2009, 16:39
tes crochets sont nuls et le terme de droite c'est Jn-2 avec un coef (mais pas celui que l'on te donne, c'est vrai)
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 16:45
par anais39600 » 01 Nov 2009, 16:45
Ericovitchi a écrit:tes crochets sont nuls et le terme de droite c'est Jn-2 avec un coef (mais pas celui que l'on te donne, c'est vrai)
je ne voi pas du tout ou est jn-2 et mes crochet ne sont pas nul je trouve pour le premier cos^pi-2/2 et (pi/2-1)sin^(pi-2/4)
je ne voi plus quoi faire dans l'enonce on me dit de me servir de la relation sin²x+cos²x=1 je vois pas du tout ou l'appliquer
si vous avez encore deux minute pour m'aider merci

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 16:52
par Ericovitchi » 01 Nov 2009, 16:52
chacun de tes crochets que tu dois prendre pour pi/2 et zéro sont des cos multipliés par des sinus
le cos s'annule pour pi/2 et le sinus pour zéro
Ton terme de droite c'est bien
(n-2)cos^{n-3}cosx dx)
?
Si c'est juste, et bien c'est
(n-2)cos^{n-2} dx = - (n-1)(n-2) J_{n-2})
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 16:55
par anais39600 » 01 Nov 2009, 16:55
Ericovitchi a écrit:chacun de tes crochets que tu dois prendre pour pi/2 et zéro sont des cos multipliés par des sinus
le cos s'annule pour pi/2 et le sinus pour zéro
Ton terme de droite c'est bien
(n-2)cos^{n-3}cosx dx)
?
Si c'est juste, et bien c'est
(n-2)cos^{n-2} dx = - (n-1)(n-2) J_{n-2})
oui cest sa je suis aller trop vite pour l'integrale je vais essayer de recommencer le tout et je posterai un autre essai
merci tout de même sa m'aide beaucoup
merci

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 16:59
par Ericovitchi » 01 Nov 2009, 16:59
un tuyau car on est sur une mauvaise piste.
Ces intégrales sont très connues ; Elles s'appellent les intégrales de Wallis.
la démo que tu cherches est par exemple là :
http://fr.wikipedia.org/wiki/Int%C3%A9grale_de_Wallisil faut effectivement détacher un cos² et le transformer en 1-sin² puis utiliser un des sin pour faire un d(cos), etc..
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 17:04
par anais39600 » 01 Nov 2009, 17:04
Ericovitchi a écrit:un tuyau car on est sur une mauvaise piste.
Ces intégrales sont très connues ; Elles s'appellent les intégrales de Wallis.
la démo que tu cherches est par exemple là :
http://fr.wikipedia.org/wiki/Int%C3%A9grale_de_Wallisil faut effectivement détacher un cos² et le transformer en 1-sin² puis utiliser un des sin pour faire un d(cos), etc..
ok merci beaucoup je vais essayer comme sa
merci beaucoup
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 17:21
par anais39600 » 01 Nov 2009, 17:21
j'ai

et je voit pas comment faire pour trouver jn= n-1/n Jn-2

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 17:26
par Ericovitchi » 01 Nov 2009, 17:26
le lien que je t'ai mis détaille tous les calculs. Je ne vais pas te les refaire ici quand même.
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 01 Nov 2009, 17:41
par anais39600 » 01 Nov 2009, 17:41
je suis d'accord pour la demonstration mais je doit partir de

et je retrouve pas

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
?
