Intégrale suite

[Anonyme]

salut

bon j'ai presque terminé de faire les intégrales que je devais faire
(plus de 300 numéro...)

je coince sur

int (cos (racine(x)) / racine (x))


int(te^(5t))


int((t^2+1) / (t^2-1))


int(1/(4-y))


int(1/(x^2+4x+d))


bon je sais que ça fait beaucoup mais bon sur 300 c'est pas si mal...
d'ailleur c'était la première fois que je touchais à ca...
--
Borland rulez
http://pages.infinit.net/borland

[rod]

ben si tu mets tout sous forme de puissance pour ta première int
ca fait : cos(x^(1/2))*x^(-1/2) la tour est joué fonction composée dérivée de x^(1/2) c'est x^(-1/2) donc on comme solution ( avec le rajout de constanstes) résultat : 2*sin(x^(1/2)


Si tu as d'autre pb n'hésite pas

[fonfon]

Salut,

int(1/(4-y))

on remarque que 1/(4-y) est de la forme -u'/u donc une primitive sera à une constante près -ln|u| +k donc ici u(y)=4-y donc une primitive sera -ln|y-4|+k

[Mikou]

pour la 3 integre par parties et la 4 tu as pour tout x dans lensemble de def de ta fonction
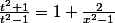
les primitives sont donc
nb : normalement en term s on n'a pas a demander cette primitive de fonction rationelle

[fonfon]

Salut ,tigri je pense qu'on integre en t et non en x

A+