Integrale de cos^4 (x)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 18:30
par youyou2 » 30 Mar 2009, 18:30
Bonjour ou Re bonjour,
Je cherche à faire cette intégrale :

Je voudrai savoir sil ya une autre méthode que par les formules d'Euler :

.
Je pense aux formules de trigo mais je voit comment sy prendre
Merci :triste:
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 30 Mar 2009, 18:33
par axiome » 30 Mar 2009, 18:33
youyou2 a écrit:
_0^(;)/4)cos^4;)(x)
Bonsoir,
Regarde
ici, qu'on comprenne ce que tu veux dire...
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 18:37
par youyou2 » 30 Mar 2009, 18:37
désolé
j'ai corrigé j'espère que c'est plus clair! :zen:
;)cos^4;)(x) de 0 à ;)/4
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 30 Mar 2009, 18:42
par Timothé Lefebvre » 30 Mar 2009, 18:42
J'édite ton post, en bon LaTeX, c'est pas mieux comme ça ?
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 18:45
par youyou2 » 30 Mar 2009, 18:45
Timothé Lefebvre a écrit:J'édite ton post, en bon LaTeX, c'est pas mieux comme ça ?
C'est clair c'est beaucoup mieux!
En fait je l'ai fait avec Word, mais quand je le copié sur votre site, il le modifié!!
Merci !!
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 19:12
par youyou2 » 30 Mar 2009, 19:12
Personne n'a une petite idée?!
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 19:15
par Euler911 » 30 Mar 2009, 19:15
Bonsoir,
Utilise ces formules:
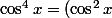^2)
Et
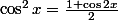
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 19:19
par Euler911 » 30 Mar 2009, 19:19
youyou2 a écrit:
Il ne faut pas oublier le "dx"... il a toute son importance!
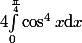
-
Black Jack
 par Black Jack » 30 Mar 2009, 19:19
par Black Jack » 30 Mar 2009, 19:19
f(x) = cos^4(x)
Comme le cos a une puissance paire, on peut s'en tirer en posant tg(x) = t
dx/cos²(x) = dt
...
1 + tg²(x) = 1/cos²(x) = 1 + t²
cos^4(x) dx = cos^6(x) dx/cos²(x)
cos^4(x) dx = dt/(1+t²)³
...
:zen:
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 19:27
par Euler911 » 30 Mar 2009, 19:27
Je ne comprends pas l'intérêt de ce changement de variable! D'autant que ledit changement ne conduit pas à une expression plus facile à intégrer...
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 19:46
par youyou2 » 30 Mar 2009, 19:46
Euler911 a écrit:Bonsoir,
Utilise ces formules:
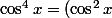^2)
Et
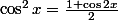
Et on obtient :
=

((1+cos;)2x)/2)²
=

(1/2)^2+ (cos;)2x/2)² de 0 à

/4
= [1/4 x + 1/8 sin;);)(4x)]

de 0 à

/4
=

/16+1/8 sin;);)(;))- 0

=

/16
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 19:49
par Euler911 » 30 Mar 2009, 19:49
Quelle horreur:P (a+b)^2=a^2+2ab+b^2 et non pas a^2+n^2!!!!
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 19:51
par Euler911 » 30 Mar 2009, 19:51
Et je le répète, le "dx" est important dans les expressions de tes intégrales!
Sans ce "dx", ce que tu écris n'a plus de sens:)
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 19:52
par youyou2 » 30 Mar 2009, 19:52
Euler911 a écrit:Quelle horreur:P (a+b)^2=a^2+2ab+b^2 et non pas a^2+n^2!!!!
Wahou la j'ai honte!
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 20:01
par Euler911 » 30 Mar 2009, 20:01
Ce n'est pas grave, ce n'est pas grave:-) Tu as droit à une seconde chance;)
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 20:03
par youyou2 » 30 Mar 2009, 20:03
J'espère que j'ai pas fait d'erreur bête!
= ;)((1+cos;)2x)/2)^2 dx
= ;)(1/2)^2+(cos;)2x/2)^ + (cos;)2x/2)^2 dx de 0 à ;)/4
= [1/4 x + 1/4 sin;);)(2x);) + 1/8 sin;);)(4x)] ;) de 0 à ;)/4
= ;)/16+1/4 sin;););)/2+ ;) 1/8 sin;);)(;))- 0 ;)
= ;)/16 + 1/4
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 20:08
par Euler911 » 30 Mar 2009, 20:08
Allez! Concentre-toi:) Je te donne encore une chance:)
Essaye d'abord de simplifier cos(x)^4 de sorte qu'il n'y ai plus de carrés. N'hésite pas à faire des mises en évidences pour t'aider à faire les calculs!
^2=\frac{1}{4}\left(1+\cos 2x\right)^2)
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 20:16
par youyou2 » 30 Mar 2009, 20:16
Euler911 a écrit:Allez! Concentre-toi:) Je te donne encore une chance:)
Essaye d'abord de simplifier cos(x)^4 de sorte qu'il n'y ai plus de carrés. N'hésite pas à faire des mises en évidences pour t'aider à faire les calculs!
^2=\frac{1}{4}\left(1+\cos 2x\right)^2)
Donc là, il faut que je dévellope par identité remarquable?
C'est ce qui j'ai fait plus haut non?!
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Mar 2009, 20:17
par Euler911 » 30 Mar 2009, 20:17
oui, c'est bien ça:) mais ce que tu as fait plus haut était faux cependant:)
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 30 Mar 2009, 20:22
par youyou2 » 30 Mar 2009, 20:22
On obtient :
= 1/4 ( 1 + 2 cos 2x + cos 4x)
??!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités



