Identifiabilité d'une fonction, pb de calcul

[Nane]

Bonjour a tous,
Je souhaiterai montrer que les paramètres d'une fonction sont identifiables, pour cela j'utilise la relation suivante [url=Identifiability]http://en.wikipedia.org/wiki/Identifiability[/url] :

Les paramètres sont identifiables SI



La fonction est de la forme suivante:

avec

(pareil pour et )


Je trouve par passage au log:



Mais la je ne sais pas comment montrer que
a_1 = a_2,
b_1 = b_2
c_1 = c_2,
d-1 = d_2,

Une idée?? :id:
Merci beaucoup,
Nane

[Nane]

Ooops :triste:

Voila ce que je trouve par passage au log (!):



Mais la je ne sais pas comment montrer que

,

Une idée?? :id:
Merci beaucoup,
Nane[/quote]

[paquito]

Ooops :triste:

Voila ce que je trouve par passage au log (!):



Mais la je ne sais pas comment montrer que

,

Une idée?? :id:
Merci beaucoup,
Nane

[/quote]

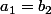
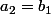
on peut déjà avoir et , donc ça ne peut pas marcher!

Tu as aussi et qui sont une possibilité parmi une infinité.

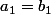
de toutes façons et entraîne
, soit une équation à 4 inconnues dont les solutions s'écrivent avec 3 paramètres arbitraires comme ; même si tu te limites aux solutions positives, tu n'as évidemment aucune chance d'arriver à montrer que:

.

[Nane]

Merci Paquito...
J'avoue ne plus trop comprendre ce qu'il se passe... dans un article, des gens arrivent a estimer ces 4 paramètres, voila pourquoi je cherchais a montrer que les paramètres sont identifiables... :mur:

Ou peut être que ma définition de l'identifiabilité n'est pas correcte ?
Merci merci,
Nane

[paquito]

J'ai regardé un ce qu'ils disent sur le net; toute cette notion intervient dans le domaine des probabilités et statistique et c'est très vite inabordable.
Le seul exemple intéressant est pour la loi normale, dont la densité dépend de 2 paramètres et (li y a déjà un 2 qui disparaît dans la démonstration).

Il faut montrer que
,

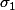
n'a lieu que lorsque et .

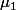
On utilise le fait qu'un polynôme de degré 2 qui s'annule pour une infinité de réels a tous ses coefficients nuls; tu peut regarder (sur wikipedia). Sinon, si on reste dans le domaine du raisonnable, tu peut prendre la loi binomiale mais tu n'auras qu'un paramètre (n est fixé) ou la loi exponentielle: densité:
; tu n'as qu'un seul paramètre. (Peut d'intérêt)

[Ben314]

Salut,
Déjà, là :

La fonction est de la forme suivante:

avec

Je ne vois pas le rapport entre ce que tu écrit et ce dont ils parlent dans le lien que tu donne où il y a une famille de fonctions dépendant d'un paramètre , mais dépendant aussi d'un x (comme toute fonction qui se respecte !!!!!!)
Elle est ou la variables de tes "fonctions" ?
Ou alors ce sont des fonctions constantes ? dans ce cas, il est clair qu'avec 4 paramètres pour un ensemble d'arrivé (=ensemble des fonctions constantes) de dimension 1, ça ne risque pas de marcher (avec une fonction continue)

Tu as pas un lien sur l'article pour qu'on puisse voir précisément de quoi il retourne ?

[Nane]

Je ne trouve pas de lien de l'article en libre acces... l'article est ICI

Effectivement, la fonction dépend de :
il s'agit plus précisement (mais en simplifié quand même) de

dans laquelles sont connus.

Les paramètres à estimer sont