Gradient

[biking]

Bonjour je bloque un peu sur la compréhension de cet exercice :

Tout d'abord on suppose que f : R2 --> R est une fonction à 2 variables dérivable sur R
2

On a 2 propositions :

P : gradient f(1, 2) =(0 , 0)

Q : (1,2) est un minimum local de f sur R2


On me demande P est il une condition nécessaire pour Q

Et on me demande aussi : P est il une condition suffisante pour Q


Dans mon correctif il est indiqué faux pour les 2 propositions

Je ne comprends pas puisque pour avoir un minimum local en (1,2) il faut absolument que le vecteur obtenu soit nul non ? J'aurais donc mis que c'est une condition nécessaire justement.

Merci d'avance

[pascal16]

Je ne suis pas spécialiste de la question, ce que je me rappelle des cours, c'est qu'on rajoutait "et de dérivée continue" (voir vers le milieu de l'article) :
https://fr.wikipedia.org/wiki/Diff%C3%A9rentielle

[capitaine nuggets]

Salut !

Dire que signifie que admet un extremum local en . Si de plus, est définie positive alors dans ce cas admet un minimum local en .

Après tu dis que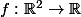 est dérivable sur , or ça n'a pas de sens.

[biking]

Excusez moi petit oublie
* dérivable sur R^{2}

du coup c'est bien une condition nécessaire non ?

[capitaine nuggets]

Ben, je ne sais pas, commence peut-être par le début : qu'est-ce qu'une condition nécessaire ?