Bonjour à tous,
Je rencontre un petit problème pour un exercice.
Voici la donnée:
On donne les points A(2 ;1) et C (9; -4) et le point O comme origine
Trouver les sommets B et D d'un carré ABCD ayant AC comme diagonale
J'ai d'abord cherché le milieu du vecteur AC, ce qui m'a donné le point M (11/2 ; -3/2)
Le vecteur AM (7/2)
(-5/2)
Depuis là, je me suis dit qu'il fallait chercher le point B -> le vecteur OM + MB = OB
De même le point D est OM + MD = OD
Enfin les vecteurs MD et MB sont perpendiculaires au vecteur AM (donc am1*md1 + am2 *md2 =0).
Mais je cale pour la réalisation.
Je vous remercie pour votre aide :jap:
Géométrie : un problème de vecteurs
5 messages
- Page 1 sur 1
Bonjour Ced111,
Tu peux aussi utiliser la rotation vectorielle comme tu sais que les diagonales d'un carré sont perpendiculaires. :lol3:
Il suffit de pivoter ton vecteur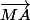 de 90°. Voici la formule complète si tu ne l'as pas :
de 90°. Voici la formule complète si tu ne l'as pas :
Le vecteur de coordonnées
de coordonnées ) a pour image par l'angle
a pour image par l'angle  le vecteur
le vecteur  de coordonnées
de coordonnées ) avec :
avec :
-y\sin(\varphi)\\<br />y' & =x\sin(\varphi)+y\cos(\varphi)<br />\end{cases})
Ici, le vecteur sera
sera 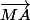 et l'angle
et l'angle  , donc
, donc 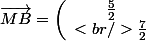) . On retrouve bien comme te l'a dit Mathelot
. On retrouve bien comme te l'a dit Mathelot 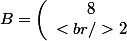) et
et  donc
donc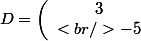)
C'est une méthode alternative... :lol3:
Voici une image pour mieux comprendre => Un carré
Voilà... :happy:
Tu peux aussi utiliser la rotation vectorielle comme tu sais que les diagonales d'un carré sont perpendiculaires. :lol3:
Il suffit de pivoter ton vecteur
Le vecteur
Ici, le vecteur
C'est une méthode alternative... :lol3:
Voici une image pour mieux comprendre => Un carré
Voilà... :happy:
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
