Généraliser : 3²+4²=5²
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zancan1337
- Messages: 5
- Enregistré le: 14 Déc 2009, 18:52
-
 par zancan1337 » 14 Déc 2009, 20:14
par zancan1337 » 14 Déc 2009, 20:14
Bonjour, premier post sur ce forum ;)
Je suis élève en 2nde et m'ennuyant un peu en cours, ma prof me donne des "prob" à bosser quand j'ai un peu de temps, pas noté mais elle "regarde car ça l'intéresse" :p
Voilà la partie de l'énoncé qui m'embête un peu (et que la prof connait pas ^^)
3²+4²=5² ; 10²+11²+12²=13²+14² ; etc
On voit qu'à chaque fois on à un terme de plus à droite et que les nombres sont des entiers qui se "suivent".
Je dois "prolonger, généraliser puis démontrer".
Pour ce je démontre d'abord pour n²+(n+1)²=(n+2)² :
n²+(n+1)²=(n+2)² <=> n²+n²+2n+1-n²-4n-4=0
n²-2n-3=0
;)=(-2)²-4(-3)=4+12=4²
n=[2+;);)]/2=3
Ou n=[2-;);)]/2=-1
J'ai donc n²+(n+1)²=(n+2)² si et seulement si n=3 ou n=-1 soit : 3²+4²=5² et (-1)²+0²=1².
Ensuite pour n²+(n+1)²+(n+2)²=(n+3)²+(n+4)² :
Même méthode (que je ne détaille pas) et même constat, 2 solutions : n=-2 ou n=10.
J'ai donc n²+(n+1)²+(n+2)²=(n+3)²+(n+4)² si et seulement si n=-2 ou n=10 soit : (-2)²+(-1)²+0²=1²+2².
Je me dis que y'aura toujours 2 solutions si on étend, mais je vais pas le faire toute ma vie...
Donc 2 questions :
-Comment exprimer le problème sans dire "2 termes = 1" ou "3 termes = 2" mais avec qqc comme n²+(n+1)²+...+(n+x)²=(n+x+1)²+...+(n+y)² où n;x;y;);) et n+1 -Comment "généraliser", étant donné que c'est pas ;)n;);) et que je n'ai que 2 solutions à chaque fois, afin de démontrer ??
Merci beaucoup ;)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Déc 2009, 20:23
par Ben314 » 14 Déc 2009, 20:23
Ta méthode n'est pas forcément la plus simple pour aboutir au résultat, mais c'est la tienne : continue sur cette voie.
Tu as :
n²+(n+1)²+...+(n+a)²=(n+a+1)²+...+(n+b)²
(je met des a et des b car en général, on prend x et y plutôt pour des réels)
mais si tu regarde les première formules, tu as un lien entre a et b (le nombre de terme à gauche et le nombre de termes à droite... ne sont pas quelconques)
Ensuite, tu peut arriver à faire quelque chose avec cette formule en développant tout les termes (et en essayant de bien te rapeller combien il y en a).
Dans les calculs, tu aurra besoin de savoir combien vaut
1+2+3+...+p=??? et aussi
1²+2²+3²+...+p²=???
Connait tu au moins la première formule ?
P.S. : Si tu ne les connait pas (ou que tu ne connait pas la deuxième), je peut te guider...
P.S.2 : En réfléchissant, je ne sais pas si c'est malin de développer les termes de ta formule. Un utilisant la deuxième somme dont je te parle, on trouve "direct" la valeur des sommes dont tu as besoin...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
zancan1337
- Messages: 5
- Enregistré le: 14 Déc 2009, 18:52
-
 par zancan1337 » 14 Déc 2009, 21:05
par zancan1337 » 14 Déc 2009, 21:05
Je connais pas ni la 1ère, ni la 2ème formule. Je dirais comme ça que la 1ère est égale à (p/2)*11 et la deuxième à heu.. aucune idée :mur: , :help: .
Pour la méthode disons que je n'ai vu que celle la...
Je vais réfléchir à ce que tu m'as dis et développer mais peut-on dév. quand on a "..." dans une expression ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Déc 2009, 21:42
par Ben314 » 14 Déc 2009, 21:42
Oui, on peut, à condition de bien maitriser ce qu'il y a dans les ...
Pour la première somme (qui n'est pas totalement utile ici)
Il suffit (plus ou moins)... de lui donner un nom... et d'une petite astuce :
Ecrit :
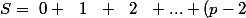+(p-1)+p)
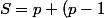+(p-2)+...+\ \ 2\ \ +\ \ 1\ \ +\ 0)
puis ajoute les deux égalitées (à droite, fait la somme colonne par colonne)
Tu trouve 2S=...
Pour vérifier que la formule est juste, il faut (évidement) regarder les premières valeurs de p :
p=0 -> 0=0
p=1 -> 0+1=1
p=2 -> 0+1+2=3
p=3 -> 0+1+2+3=6
p=4 -> 0+1+2+3+4=10
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
zancan1337
- Messages: 5
- Enregistré le: 14 Déc 2009, 18:52
-
 par zancan1337 » 14 Déc 2009, 21:58
par zancan1337 » 14 Déc 2009, 21:58
Ok merci :D
Je bosse ça demain en cours et je mettrai après ce que j'ai pas compris ;)
Merci beaucoup!
-
maturin
- Membre Irrationnel
- Messages: 1193
- Enregistré le: 09 Nov 2006, 16:28
-
 par maturin » 14 Déc 2009, 22:40
par maturin » 14 Déc 2009, 22:40
sinon tu as la propriété suivante:
un polynome ax²+bx+c avec a et c de signes différents a deux racines réelles de signes opposées.
Ce qui se démontre facilement (delta>0 et c/a=produit des racines)
donc si on prends ta formulation:
n²+(n+1)²+...+(n+x)²=(n+x+1)²+...+(n+y)²
qu'on met tout du meme coté:
[n²+(n+1)²+...+(n+x)²]-[(n+x+1)²+...+(n+y)²]
si tu veux mettre ça sous la forme an²+bn+c que vaut a (quel est son signe ?) et quel est le signe de c.
Pas besoin de développer et d'utiliser les formules pour trouver les signes.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Déc 2009, 22:49
par Ben314 » 14 Déc 2009, 22:49
Salut maturin,
Perso., je pensait qu'il voulait la (les) valeur(s) de n (en fonction de a) et, en particulier montrer que n... est entier.
Dans ce cas, je pense qu'il faut... un peu se salir les mains...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
zancan1337
- Messages: 5
- Enregistré le: 14 Déc 2009, 18:52
-
 par zancan1337 » 14 Déc 2009, 22:56
par zancan1337 » 14 Déc 2009, 22:56
@maturin : merci ;)
Je voudrais tout ce que je peux tirer de cette expression : la généraliser, la démontrer, exprimer n en fonction de a dans un cas "...", ect
Je me sers de ça pour apprendre des ptites choses (ce que ne permet pas une classe de 35 avec 6.5 de moyenne en maths ^^).
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Déc 2009, 10:55
par benekire2 » 15 Déc 2009, 10:55
En fait ton expression se ramène à cela: ( si je ne m'abuse ...)
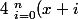^2=\Bigsum_{i=0}^{n-1}(x+n+1+i)^2)
Si je te comprend bien, tu veut montrer que cette équation admettra toujours deux solutions quelque soit n de N ?
Une seule certitude : Ce n'est pas simple.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Déc 2009, 11:02
par Ben314 » 15 Déc 2009, 11:02
Ce n'est pas si méchant que ça... modulo de commencer par chercher combien vaut 0²+1²+2²+3²+...+p²
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Déc 2009, 11:08
par benekire2 » 15 Déc 2009, 11:08
(2p + 1)}{6})
pour la suite ... j'ai pas trop cherché ...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Déc 2009, 11:10
par Ben314 » 15 Déc 2009, 11:10
Oui,
(2p + 1)}{6})
Sait tu démontrer cette formule ? (je me proposait de le guider pour qu'il la trouve)
Evidement, je ne veut pas une preuve par récurrence car pour faire une récurrence, il faut connaitre le résultat !
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Déc 2009, 11:24
par benekire2 » 15 Déc 2009, 11:24
Oui ca se démontre sans récurrence assez aisément
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Déc 2009, 11:33
par benekire2 » 15 Déc 2009, 11:33
Pour un bon seconde qui a quelques notions en polynômes ça doit pouvoir se faire :
on cherche un polynôme de degré 3 qui vérifie P(x+1)-P(x)=x² avec P(1)=0
On procède par identification.
Et grâce à notre nouvelle écriture de x² on arrive sur 1²+2²+...+n²= P(n+1)
qui vaut
(2n+1)}{6})

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Déc 2009, 11:40
par Ben314 » 15 Déc 2009, 11:40
Tout à fait,
Mais, je vient de me rendre compte que , si on écrit l'équation que l'on veut résoudre sous la forme (astucieuse) :
^2+(n-a+1)^2+...+(n-1)^2+n^2=(n+1)^2+(n+2)^2+...+(n+a-1)^2+(n+a)^2)
et que l'on développe alors il n'y a plus besoin de savoir combien vaut 1²+2²+...+p² car les termes de cette forme... s'éliminent !
(ce qui est normal car, comme n=0 est une solution, le polynôme du second degrés que l'on doit trouver est... sans terme constant)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Déc 2009, 11:44
par Ben314 » 15 Déc 2009, 11:44
Si tu veut une seconde méthode pour trouver 0²+1²+...+p² (que je trouve 'plus jolie'), développe (a+1)^3 puis écrit l'un en dessous de l'autre :
1^3=(0+1)^3=...
2^3=(1+1)^3=...
3^3=(2+1)^3=...
.
.
.
(p+1)^3=...
où, a droite des = tu écrit la formule que tu as trouvé pour (a+1)^3 en remplacant a par 0,1,... et surtout en ne faisant aucun calcul.
Ensuite tu fait la somme de toutes ces égalités...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Déc 2009, 11:56
par benekire2 » 15 Déc 2009, 11:56
oui, et quand on réduit il me semble que l'on arrive sur :
quelque chose comme : -4na-4n(a-1)-4n(a-2) - ... - 4n+n²=0
Joli la méthode :++:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Déc 2009, 12:07
par Ben314 » 15 Déc 2009, 12:07
Je me demandais si, pour être sympa avec zancan1337, il faudrait pas enlever tout nos posts et en mettre un seul lui indiquant l'équation astucieuse (peut être avec a d'un coté et b de l'autre en lui demandant de trouver b pour qu'il y ait un terme de plus à gauche que à droite)
et en lui disant qu'il suffit alors de connaitre 1+2+...+p.
Qu'en pense tu ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Déc 2009, 14:51
par benekire2 » 15 Déc 2009, 14:51
Faut le laisser chercher ( le bon post ) :ptdr:
Il devrait s'en sortir :id:
-
zancan1337
- Messages: 5
- Enregistré le: 14 Déc 2009, 18:52
-
 par zancan1337 » 17 Déc 2009, 10:51
par zancan1337 » 17 Déc 2009, 10:51
Ouai je m'en sort ;) Je fini ce week-end je pense. Par contre, les trucs comme benekire2 avec des expressions en LaTex, ça me largue un peu ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 197 invités
