Fonction trigonométrique côté graphique

[alex-blade2]

Bonjour, j'ai un DM à résoudre, mais dans le 1er exercice je bloques sur 2 questions, ou a vrai dire je ne sais pas trop comment répondre, je vous explique :
Il nous est donné la fonction f(x)=2cos(x) +x

Dans les premières questions ont obtient le tableau de variation de f qui est : croissant sur [-pi;pi/6] et sur [5pi/6;pi] décroissant sur [pi/6;5pi/6]. On trouve aussi que sur I = [-pi;pi], f(x)=0 admet une unique solution alfa.

La question à laquelle je bloque c'est : Montrer que sur IR l'équation f(x)=0 admet alfa comme unique solution.
D'après la calculette je vois que la Cf est strictement croissante et donc qu'elle coupera l'axe des abscisses une seule fois (alfa) mais je sais pas comment le prouver.


La deuxième question à laquelle je bloque c'est :
Montrer que le vecteur MM', où M est un point d'abscisse x (x appartient IR) de Cf et M' le point d'abscisse x+2pi de Cf, est un vecteur constant, indépendant du choix du point M.
Comment, connaissant Cf sur I, peut-on en déduire Cf sur IR ?

Pour cette question c'est obscur je ne comprends pas trop l'histoire des vecteurs.

Merci de votre aide d'avance.

[Mortelune]

Bonjour

Montrer que sur IR l'équation f(x)=0 admet alfa comme unique solution.

Normalement il va falloir utiliser la dérivée, peut être des valeurs de f en cas de non stricte monotonie de f, et agrémenté du théorème des valeurs intermédiaires.

Montrer que le vecteur MM', où M est un point d'abscisse x (x appartient IR) de Cf et M' le point d'abscisse x+2pi de Cf, est un vecteur constant, indépendant du choix du point M.
Comment, connaissant Cf sur I, peut-on en déduire Cf sur IR ?

Tu peux essayer d'observer la périodicité du cosinus.

[alex-blade2]

En faite j'ai déjà démontré à l'aide de la dérivée qu'il y avait une solution alfa sur [-pi;pi] pour f(x)=0, je pensais qu'il suffisait d'une étape pour passer de l'intervalle I à IR ?

Cosinus est périodique de période 2pi, mais je ne vois pas comment mener à bien cette question ?

[Mortelune]

Donc dans la première il suffit de montrer que pour x n'appartenant pas à l'intervalle ta fonction est soit toujours négative soit toujours positive et le tout strictement, du coup tu auras montré qu'elle ne s'annulera pas ailleurs.

Pour la 2 tu as M(x,f(x)) et M'(x+2pi,f(x+2pi)) du détermines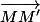 comme tu déterminerais pour A et B fixés

[alex-blade2]

Je vais travailler tout ça au brouillon, je reviendrais si d'autres problèmes ce posent, je te remercie.

[alex-blade2]

Comment est-ce que je peux montrer que je peux démontrer que lorsque x n'appartient pas à l'intervalle alors la foncion est strictement positive ou négative, je ne vois pas ?

[Mortelune]

L'intervalle considéré est .

f(x)=2cos(x) +x.

et comme (en utilisant un encadrement du cosinus) et que on a f<0 sur

Ensuite il faut faire la même chose sur l'autre l'intervalle

[alex-blade2]

Je ne comprends pas cette étape : et que f(x)=x² en faite je vois pas d'où arrive le x² car f(x) n'est pas égale a x².

[Mortelune]

L'intervalle considéré est .

f(x)=2cos(x) +x.

et comme (en utilisant un encadrement du cosinus) et que on a f<0 sur

Ensuite il faut faire la même chose sur l'autre l'intervalle

C'est un problème de balise, pas étonnant que tu comprennes pas j'avais écris ça : -\pi<2.

Donc j'ai modifié la syntaxe dans la citation.

[alex-blade2]

Mais si -pi < 2 et que f(x) < 2+x ça veut dire que f(x) > 0, je comprends pas pourquoi il est inférieur alors ici ?

[Mortelune]

Regarde bien l'intervalle choisi ;)

[alex-blade2]

Oui en effet c'est bon merci beaucoup. Je m'attaques maintenant aux vecteurs, restes dans le coin je pense que j'aurai besoin de tes lumières.

[alex-blade2]

J'ai tout fini merci beaucoup à toi Mortelune.