Dp fonction/théorème de Ceva

[steste]

Bonsoir,
J'ai un Dp a faire sur les fonctions de fonctions (F o g) etc. Mais aussi sur les Vecteurs et le barycentre.
Je suis un peu perdu sur les barycentres !
J'ai commencer à me pencher dessus cependant je voudrais d'abord savoir si le premier exercice est juste avant de me lancer dans le deuxième !


Voici le sujet




Pour le premier exercice voila ce que je trouve:

1)a) f(x)=0
1-x²=0
=>1=x²
=>V1=x
x=1
x=-1
b) même démarche pour f(x)>=0

2)g(x)=f(f(x=)
g(x)=1-(1-x²)²

Est ce correct ?
Si oui alors je suppose que pour le c) --> h(x)=1-[1-(1-x²)²]²


Merci Par avance

[kushiki]

Bonsoir,

C'est exactement ca.
Bonne continuation.

[steste]

Bonjour,
Voila je bloque lorsqu'il faut factoriser g(f(f(x)))

g(x)=f(f(x))=1-(1-x²)²


1-(1-x²)²=0
[1-(1-x²)][1+(1-x²)]=0
-x²(2-x²)=0

Comment je fait après ?
Merci par avance

[kushiki]

Bonjour,

en fait tu es dans la bonne voie.
Il faut que tu t'arrêtes à [1-(1-x²)][1+(1-x²)]=0
A partir de là c'est comme si tu avais (1-X)(1+X)=0 avec X=(1-x²)
donc soit (1-X)=0 soit (1+X)=0
après à toi de résoudre.

[angel-91]

Bonjour
désolé de vous déranger
mais j'ai besoin d'aide pour mon exrcice http://maths-forum.com/showthread.php?t=94564

Merci

[steste]

angel-91 On a tous besoin d'aide, ce n'est pas la peine de faire du rentre dedans à tout le monde, il y a des gens qui sont là pour nous aider !

kushiki merci de ton aide, je vais travailler dessus !

EDIT de la modération : tu as tout à fait raison, son message a été supprimé.

[steste]

Bonsoir,
J'arrive à

[1-(1-x²)][1+(1-x²)]=0
X=(1-x²)
[1-X][1+X]=0
Donc
X=1 ou X=-1

X=(1-x²)

(1-x²)=1 ou (1-x²)=-1
-x²=0 ou -x²=-2
x=0 ou x=V2

Est-ce correct ?
Merci par avance

[kushiki]

bonsoir,
désolée pour la réponse tardive.
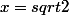
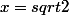
Oui c'est presque correcte : pour x²=2 ce n'est pas tout à fait c'est soit ou .

Voilà.
Bon courage!

[steste]

Bonsoir, merci de votre réponse, mais en faisant une autre méthode je suis bien tombé sur ces réponses,

Voici mais autres réponses, pour le 2)b)

tableau de signe

x -infini -V2 0 V2 +infini
g(x) - 0 + 0 + 0 -

Donc g(x)>=0
S=[-V2;V2]

3)a)
h(x)=f(f(f(x)))=1-[1-(1-x²)²]²

1-[1-(1-x²)²]²=0
(1-[1-(1-x²)²])(1+[1-(1-x²)²])=0
Et la je bloque, en fait j'ai continuer au brouillon mais voila sur quoi je tombe:
(-(1-x²)²)(2-1-x²)²)=0
[-(1-x²)²][2-(1-x²)][2+(1-x²)]=0
et la je trouve comme solution -(1-x²)=0 ou (1-x²)=0 ou 2-(1-x²)=0 ou 2+1-x²=0
Après donc
x=V1 ou x= V3
Donc
x=-1 ou x=-V3
x=1 ou x=V3

Mais je pense que c'est faux !

Maintenant pour L'exercice 2,je suis complètement perdu, je n'y arrive absolument pas avec les barycentres, si vous pouviez m'aiguiller sur la bonne voie cela serait gentil de votre part !