Fonction qui tend vers e

[sim80000]

Bonjour,

Je voudrais savoir si il existe une autre fonction que f(x)=(1+1/x)^x qui tend vers e.
sans ajouter e dans la fonction...c'est trop facile
Merci

[Lostounet]

Bonjour,

Je voudrais savoir si il existe une autre fonction que f(x)=(1+1/x)^x qui tend vers e.

Merci

La fonction f(x)=e+1/x

[WillyCagnes]

bonjour à tous
autre exemple: f(x)= e - e^-x

[Pseuda]

Bonsoir,

Par contre il y a 2 suites qui tendent vers e : (1+1/n)^n et 1+1/1!+1/2!+1/3!+....+1/n!.

Forcément elles ne contiennent pas e, nombre irrationnel et même non algébrique.

[Lostounet]

Ou alors

F(x) = (sin(1/x)*x+1/ln(x))^(ln(x))

[Tiruxa47]

Une suite qui ne fait pas intervenir de fonctions ....

Elle utilise les permutations ne n éléments Pn et les dérangements Dn de n éléments.

Un dérangement étant une permuation où aucun élément ne retrouve sa place initiale.

La suite Pn/Dn a pour limite e.
La convergence est rapide pour n= 7 on a déjà 2.718...

Pour la démo :
https://elbenaroya.files.wordpress.com/ ... ations.pdf

[Ben314]

Sinon, y'a ça :

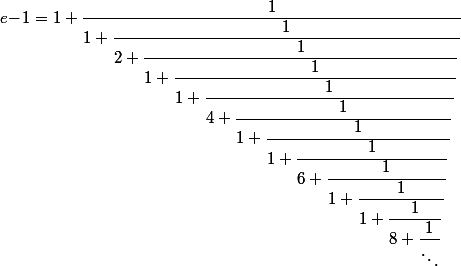
Qui donne les "meilleures" approximations de sous forme de fraction, par exemple à près ;
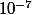
à près ; à près ; à près . . .