Fonction logarithme
20 messages
- Page 1 sur 1
Fonction logarithme
Bonjour, je suis bloqué sur un problème, il faut prouver que:
10^3log(x)+2 = 100x^3
Si quelqu'un peut m'aider,
Merci d'avance
10^3log(x)+2 = 100x^3
Si quelqu'un peut m'aider,
Merci d'avance
Re: Fonction logarithme
Bonjour,
Quelle est la base du logarithme ?
Tu peux te servir de cette propriété du logarithme :
=p.log_b(x))
En d'autres termes :
=log(x^{10^{3}}))
Par propriété des puissances :
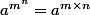
Donc :
=log_b(x^{30}))
On reprend l'équation de base :
+2=log_b(x^{30})+2)
+2=100x^3)
Donc on a :=100x^3-2)
Après c'est relativement simple. Il te faut la base de ton logarithme (si ce n'est pas le logarithme népérien) car une des propriétés essentielles des log est :
=\frac{ln(x)}{ln(b)})
On va juste montrer que le premier membre de l'équation est égal au second. Ou alors montrer directement :+2=100x^3)
Donc que}{ln(b)}+2=100x^3)
En espérant avoir pu aider un petit peu
Quelle est la base du logarithme ?
Tu peux te servir de cette propriété du logarithme :
En d'autres termes :
Par propriété des puissances :
Donc :
On reprend l'équation de base :
Donc on a :
Après c'est relativement simple. Il te faut la base de ton logarithme (si ce n'est pas le logarithme népérien) car une des propriétés essentielles des log est :
On va juste montrer que le premier membre de l'équation est égal au second. Ou alors montrer directement :
Donc que
En espérant avoir pu aider un petit peu
Re: Fonction logarithme
Le problème c'est que nous n'avons pas vu toutes ces formules, j'avais trouvé une réponse mais je ne suis pas sure qu'elle marche. J'avais fait:
10^3log(x)+2 = 10 ^log(x^3)+log(100) = 10 ^log(100x^3)
10^log(100x^3)= log(10^100x^3) = 100x^3^log10 et 100x^3^log10 = 100x^3
Mais je ne suis pas sure que cela soit possible de déplacer les log de comme ça
Merci d'avance
10^3log(x)+2 = 10 ^log(x^3)+log(100) = 10 ^log(100x^3)
10^log(100x^3)= log(10^100x^3) = 100x^3^log10 et 100x^3^log10 = 100x^3
Mais je ne suis pas sure que cela soit possible de déplacer les log de comme ça
Merci d'avance
Re: Fonction logarithme
Bonsoir
Je pense que anonymous84 voulait dire
10^(3log(x)+2)
dans ce cas la première étape est
10^(a+b)=10^a . 10^b
log désigne le logarithme décimal
A vous ...
Je pense que anonymous84 voulait dire
10^(3log(x)+2)
dans ce cas la première étape est
10^(a+b)=10^a . 10^b
log désigne le logarithme décimal
A vous ...
Re: Fonction logarithme
Non c'est 10^(3\log (x)+2) = 10 ^(log (x^3) + log (100))
En fait tout le calcul est exposé en puissance
En fait tout le calcul est exposé en puissance
Re: Fonction logarithme
Merci pour l'éclairage.
Donc pour donner une piste si je ne m'abuse et Rdvn dites moi si je me trompe :
+2}\iff 10^{3.log(x)}\times 10^{2}\iff 10^{log(x^{3})} \times100)
Or pour tout log de base b, la fonction réciproque est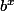 .
.
Donc effectivement le calcul est juste car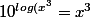
Donc pour donner une piste si je ne m'abuse et Rdvn dites moi si je me trompe :
Or pour tout log de base b, la fonction réciproque est
Donc effectivement le calcul est juste car
Re: Fonction logarithme
Pourquoi y a-t-il à présent 3\log(x) ?
Absent de l'énoncé
Qui d'ailleurs signifierai quoi ?
De quoi parlez vous au juste ?
Mettez les parenthèses où il en faut
Avec le résultat attendu, mon énoncé convient ...
Absent de l'énoncé
Qui d'ailleurs signifierai quoi ?
De quoi parlez vous au juste ?
Mettez les parenthèses où il en faut
Avec le résultat attendu, mon énoncé convient ...
Re: Fonction logarithme
@MaynaMilano
oui mais ce sont des égalités, pas des équivalences
Mais anonymous84 avait modifié son énoncé
Donc
Avec mon énoncé, le résultat attendu, vos calculs mais avec =, on arrive à quelque chose de cohérent
Est ce OK ?
oui mais ce sont des égalités, pas des équivalences
Mais anonymous84 avait modifié son énoncé
Donc
Avec mon énoncé, le résultat attendu, vos calculs mais avec =, on arrive à quelque chose de cohérent
Est ce OK ?
Re: Fonction logarithme
Désolé, c'est une erreur de frappe
En effet, la première étape est: 10^(a+b)=10^a . 10^b
Donc dites moi si je me trompe mais cela donne: 10^(3log(x)) X 10^2
Ensuite je dois faire quoi ?
En effet, la première étape est: 10^(a+b)=10^a . 10^b
Donc dites moi si je me trompe mais cela donne: 10^(3log(x)) X 10^2
Ensuite je dois faire quoi ?
Re: Fonction logarithme
Eh bien
10^2=100
et pour 10^(3log(x)) voyez la réponse de MaynaMilano (mettre = au lieu de <=>)
Que proposez vous ?
10^2=100
et pour 10^(3log(x)) voyez la réponse de MaynaMilano (mettre = au lieu de <=>)
Que proposez vous ?
Re: Fonction logarithme
bonsoir,
log() désigne le logarithme décimal.
on a
}=\left( 10^{log(x)} \right) ^3)
}=x^3)
d'où
+2}=10^{3 log(x)} \times 10^2= x^3 \times 100 = 100 x^3)
en effet,) et
et 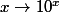 sont des bijections réciproques l'une de l'autre , si bien que:
sont des bijections réciproques l'une de l'autre , si bien que:
}=x) pour x>0
pour x>0
=x) pour x réel
pour x réel
log() désigne le logarithme décimal.
on a
d'où
en effet,
Modifié en dernier par mathelot le 19 Jan 2022, 18:10, modifié 1 fois.
Re: Fonction logarithme
Donc 10^(3log(x) + 2) = 10^log(x^3) X 100
et 10^log(x^3) = x^3 donc x^3 X 100 = 100x^3
Est-ce bien juste ?
et 10^log(x^3) = x^3 donc x^3 X 100 = 100x^3
Est-ce bien juste ?
Re: Fonction logarithme
@anonymous84
Votre dernière réponse est correcte (x>0 en énoncé, je présume)
C'est celle que j'attendais de votre part, après mon indication, conformément à la charte du forum.
Voilà qui est fait
Bonne soirée
@MaynaMilano
Voyez la différence entre = et <=>
Revenez sur le forum au besoin
Bonne soirée
Votre dernière réponse est correcte (x>0 en énoncé, je présume)
C'est celle que j'attendais de votre part, après mon indication, conformément à la charte du forum.
Voilà qui est fait
Bonne soirée
@MaynaMilano
Voyez la différence entre = et <=>
Revenez sur le forum au besoin
Bonne soirée
Re: Fonction logarithme
MaynaMilano a écrit:Par propriété des puissances :
cette égalité est fausse car
Re: Fonction logarithme
@anonymous84
Il faut tout rentrer dans le log derrière la puissance de 10 afin de les "faire disparaître" : 10^log(X) =X car le log est "l'opération contraitre" de 10^.
Il faut tout rentrer dans le log derrière la puissance de 10 afin de les "faire disparaître" : 10^log(X) =X car le log est "l'opération contraitre" de 10^.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
