Dm fonction exponentielle
40 messages
- Page 2 sur 2 - 1, 2
OK mais je sais pas si tu sais mais la je suis en train de faire la 3/ a).
Tu es bien en train de m'aider pour celle-là, parce que là c'est très confus pour moi....
non, je t'ai aider pour 2)a,b,c car tu n'etais pas sûr de ce que tu avais fait donc c'etait pour t'aider à y voir un peu plus clair
pour la 3a)
on te dit de te servir de la relation
essaie de faire un petit changement devariable en posant
non, il faut te servir de ton encadrement
pour montrer que y=ax+b est asymptote à la courbe il faut calculer la lim f(x)-(ax+b) et montrer que ça vaut 0
or ici tu as
\le\frac{1}{2x})
et

theoreme des gendarmes
-x\ge\frac{-1}{2x}) donne
donne -x=0)
donc la droite delta d'equation y=.... est asymptote au voisinage de +inf
apres pour la position elative il faut etudiaer le signe de f(x)-x....
pour montrer que y=ax+b est asymptote à la courbe il faut calculer la lim f(x)-(ax+b) et montrer que ça vaut 0
or ici tu as
et
theoreme des gendarmes
donc la droite delta d'equation y=.... est asymptote au voisinage de +inf
apres pour la position elative il faut etudiaer le signe de f(x)-x....
l'equation de la tangente est donnée pas la formule que je t'ai ecrit,tu devrais l'avor quelque part dans ton cours
tu connais}=(x+1)e^{-\frac{1}{x}})
il te faut f(a) tu remplaces x par a soit
}=(a+1)e^{-\frac{1}{a}})
de plus tu as dejà calculer
}=\frac{e^{-\frac{1}{x}}(x^2+x+1)}{x^2})
il te faut f'(a) donc tu remplaces x par a soit
}=\frac{e^{-\frac{1}{a}}(a^2+a+1)}{a^2})
donc comme l'equation de la tangente à C est donnée par la formule suivante:
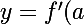(x-a)+f(a))
il suffit de remplacer et on abotient:
}{a^2}(x-a)+(a+1)e^{-\frac{1}{a}})
en reduisant au même denominateur on obtient:
x-a)}{a^2})
pour la suite qu'elle est l'equation de l'axe des abscisses?
tu connais
il te faut f(a) tu remplaces x par a soit
de plus tu as dejà calculer
il te faut f'(a) donc tu remplaces x par a soit
donc comme l'equation de la tangente à C est donnée par la formule suivante:
il suffit de remplacer et on abotient:
en reduisant au même denominateur on obtient:
pour la suite qu'elle est l'equation de l'axe des abscisses?
Baba a écrit:Donc je garde tout ca pour faire office d'équation de Ta ?!?!!
Par contre je n'ai pas bien compris pourquoi tu me demandes l'équation de l'axe des abscisses, et puis je ne sais pas vraiment quelle est cette équation....
y=0 ??
oui, garde tout ça si tu veux sinon tu peux juste utiliser directement f(a),f'(a) et la formule de l'equation moi j'ai fait tout ça pour te le detailler
je t'ai demander l'equation de l'axe des abscisses car dans la question b) on te demande de montrer que la tangente Ta coupe l'axe des abscisses (Ox) au point d'abscisse x=a/(a²+a+1)
et oui l'equation de l'axe des abscisses c'est y=0
il faut donc que tu resolves
pour trouver ce qui est demandé
40 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
