Fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:00
par Emy-Elyna » 13 Oct 2012, 14:00
Bonjour a tous, j'ai un exercice de maths à faire. Je viens à peine de commencer les fonctions exponentielles et j'ai beaucoup de mal.
Énonce:
Pour k réel, on considère la fonctions f de k définie sur R pas f de k (x)=(x+1)e puissance(kx)
1- qu'elle est la nature de f de 0
(J'ai mis fonction affine)
2- déterminer les limites de f de k en -l'infini et +l'infini en distinguant les cas k0
3- étudier le signe de (x+1) (e puissance x -1)
En déduire la position relatives des courses représentant les fonctions f de k et f de k+1.
4- étudier le sens de variation de f de k pour k<0 et k>0
Merci d'avance de votre aide !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:04
par Kikoo <3 Bieber » 13 Oct 2012, 14:04
Emy-Elyna a écrit:Bonjour a tous, j'ai un exercice de maths à faire. Je viens à peine de commencer les fonctions exponentielles et j'ai beaucoup de mal.
Énonce:
Pour k réel, on considère la fonctions f de k définie sur R pas f de k (x)=(x+1)e puissance(kx)
1- qu'elle est la nature de f de 0
(J'ai mis fonction affine)
2- déterminer les limites de f de k en -l'infini et +l'infini en distinguant les cas k0
3- étudier le signe de (x+1) (e puissance x -1)
En déduire la position relatives des courses représentant les fonctions f de k et f de k+1.
4- étudier le sens de variation de f de k pour k0
Merci d'avance de votre aide !
Salut,
(x)=(x+1)e^{k(x)})
, n'est-ce pas ? La façon dont tu as formulé l'exo me semble bien obscure.
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:08
par Emy-Elyna » 13 Oct 2012, 14:08
Je vais sur mon Ordi pour une meilleure écriture. Et je te réécrit tout ca. :) merci de bien vouloir m'aider
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:16
par Emy-Elyna » 13 Oct 2012, 14:16
Pour k réel, on considère la fonctions fk définie sur R pas f de k(x)=(x+1)e (kx)
1- qu'elle est la nature de f0
2- déterminer les limites de f de k en -l'infini et +l'infini en distinguant les cas k0
3- étudier le signe de (x+1) (e x - 1)
En déduire la position relative des courses représentant les fonctions f de k et f de k+1.
4- étudier le sens de variation de f de k pour k<0 e
Jai mis
1- F0(x)= (x+1)e(0x)
=(x+1) 1x car e0=1
Comme 1x sera toujours egale à 1 quel que soit la valeur de x
= x+1
Cette fonction est donc une fonction affine.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:25
par Kikoo <3 Bieber » 13 Oct 2012, 14:25
Emy-Elyna a écrit:Pour k réel, on considère la fonctions fk définie sur R pas f de k(x)=(x+1)e (kx)
1- qu'elle est la nature de f0
2- déterminer les limites de f de k en -l'infini et +l'infini en distinguant les cas k0
3- étudier le signe de (x+1) (e x - 1)
En déduire la position relative des courses représentant les fonctions f de k et f de k+1.
4- étudier le sens de variation de f de k pour k<0 e
Jai mis
1- F0(x)= (x+1)e(0x)
=(x+1) 1x car e0=1
Comme 1x sera toujours egale à 1 quel que soit la valeur de x
= x+1
Cette fonction est donc une fonction affine.
"f de k de x" ?
S'agirait-il d'une composée de fonctions ?
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:26
par Emy-Elyna » 13 Oct 2012, 14:26
non c'est f petit k de (x)
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:28
par Kikoo <3 Bieber » 13 Oct 2012, 14:28
Emy-Elyna a écrit:non c'est f petit k de (x)
oulah, j'ai du mal à comprendre... :hum:
S'agirait-il de
)
?
))
?
)
?
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:29
par Emy-Elyna » 13 Oct 2012, 14:29
la première !
comment fait tu as écrire ainsi ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:33
par Kikoo <3 Bieber » 13 Oct 2012, 14:33
J'utilise le LaTeX, logiciel pour écrire des formules mathématiques :) Tu peux voir un didacticiel écrit par Uztop sur la première page de la section lycée ! Il te permettra de vite t'habituer au TeX.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:34
par Kikoo <3 Bieber » 13 Oct 2012, 14:34
Bref, on a
=(x+1)e^{kx})
, je me trompe ?
Alors k est une constante/un paramètre. x est la variable.
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:37
par Emy-Elyna » 13 Oct 2012, 14:37
oui c'est ca.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:38
par Kikoo <3 Bieber » 13 Oct 2012, 14:38
Ok,
Quand x vaut 0, que vaut l'expression
)
?
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:39
par Emy-Elyna » 13 Oct 2012, 14:39
la premiere question je l'ai faite !
j'ai besoin d'aide pour la deuxieme
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:46
par Kikoo <3 Bieber » 13 Oct 2012, 14:46
Eh bien non, je ne suis pas d'accord avec ta réponse pour la question 1 !
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:47
par Emy-Elyna » 13 Oct 2012, 14:47
pourquoi ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 13 Oct 2012, 14:48
par Luc » 13 Oct 2012, 14:48
Kikoo <3 Bieber a écrit:Bref, on a
=(x+1)e^{kx})
, je me trompe ?
Alors k est une constante/un paramètre. x est la variable.
)
est une famille de fonctions à un paramètre réel. En fait, c'est équivalent à une fonction de deux variables réelles, tout est une question de point de vue. En informatique, le passage d'une fonction de deux variables à une famille de fonctions d'une variable à un paramètre s'appelle la curryfication.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 13 Oct 2012, 14:51
par Luc » 13 Oct 2012, 14:51
Kikoo <3 Bieber a écrit:Eh bien non, je ne suis pas d'accord avec ta réponse pour la question 1 !
Je pense que l'énoncé est plutôt : "quelle est la nature de
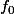
", ce qui expliquerait la réponse, qui est correcte.
/offtopic
Et sinon, ce DS?
/offtopic
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:51
par Emy-Elyna » 13 Oct 2012, 14:51
oui mais 0 remplacerait le k
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Oct 2012, 14:51
par Kikoo <3 Bieber » 13 Oct 2012, 14:51
Luc a écrit:)
est une famille de fonctions à un paramètre réel. En fait, c'est équivalent à une fonction de deux variables réelles, tout est une question de point de vue. En informatique, le passage d'une fonction de deux variables à une famille de fonctions d'une variable à un paramètre s'appelle la curryfication.
Salut Luc !
Il me semble que le paramétrage s'effectue sur k sans ambiguité dans notre cas.
-
Emy-Elyna
- Membre Naturel
- Messages: 17
- Enregistré le: 13 Oct 2012, 13:51
-
 par Emy-Elyna » 13 Oct 2012, 14:53
par Emy-Elyna » 13 Oct 2012, 14:53
tout à fait Luc.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
