Factoriser sans identitées remarquables ou facteur commun ? !HELP!

[Agathe-72]

Bonsoir,

J'ai à factoriser des expressions, pour la majeure partie aucun problème, simplement
celle-ci me pose problème :

x²-6x +5

Je pensais à la base utiliser la formule (a+b)² = a² + 2ab + b² hors pour cela mon 5 aurait du être un 3, je ne sais plus par quel bout prendre mon exo si quelqu'un est en mesure de m'aider ... merci !

[ampholyte]

Bonjour,

Est-ce que tu peux trouver une solution simple pour résoudre : x² - 6x + 5 = 0?

[Agathe-72]

Bonjour,

Est-ce que tu peux trouver une solution simple pour résoudre : x² - 6x + 5 = 0?

Je ne sais pas sans trouver Delta, voir si celui ci est positif, negatif ou egal à 0, il y a d'autre solutions ?

[ampholyte]

On peut rapidement voir que x = 1 fonctionne (racine évidente).

Cela signifie que l'on peut écrire x² - 6x + 5 sous la forme de (x - 1)(x + a) que vaut a ?

Mais sinon tu peux également calculer les racines à partir du discriminant et te souvenir que

ax² + bx + c = (x - x1)(x - x2) avec x1 et x2 les racines du polynôme.

[Agathe-72]

On peut rapidement voir que x = 1 fonctionne (racine évidente).

Cela signifie que l'on peut écrire x² - 6x + 5 sous la forme de (x - 1)(x + a) que vaut a ?

Mais sinon tu peux également calculer les racines à partir du discriminant et te souvenir que

ax² + bx + c = (x - x1)(x - x2) avec x1 et x2 les racines du polynôme.

Je ne connais pas tout ca, je suis un peu perdue là :/

[chan79]

Je ne sais pas sans trouver Delta, voir si celui ci est positif, negatif ou egal à 0, il y a d'autre solutions ?

tu peux remplacer 5 par 9-4

x²-6x+5 = x²-6x +( 9-4)= (x²-6x+9)-4=(x-3)²-2²

[ampholyte]

Bon reprenons avec la méthode du discriminant.

Pour factoriser ax² + bx + c on cherche ces racines.



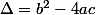
Si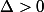 alors il y a 2 racines réelles






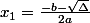
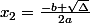
On peut donc réécrire : ax² + bx + c = (x - x1) (x - x2)

(tu pourras le vérifier en redéveloppant sur ton exercice).

Si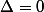 alors une racine réelle double



On peut donc factoriser : ax² + bx + c = (x - xo)²

Si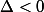 pas de factorisation possible dans R

[Agathe-72]

tu peux remplacer 5 par 9-4

x²-6x+5 = x²-6x +( 9-4)= (x²-6x+9)-4=(x-3)²-2²

J'ai très bien compris ta démarche, simplement le resultat final n'est pas une factorisation réelle puisque il y a encore un moins, je me trompe ?

[chan79]

J'ai très bien compris ta démarche, simplement le resultat final n'est pas une factorisation réelle puisque il y a encore un moins, je me trompe ?

c'est qu'il te reste à terminer; c'est une différence de carrés
a²-b²=(a-b)(a+b)
le a, c'est (x-3)
le b, c'est 2

[Agathe-72]

c'est qu'il te reste à terminer; c'est une différence de carrés
a²-b²=(a-b)(a+b)
le a, c'est (x-3)
le b, c'est 2

Merci du coup je trouve

x²-6x+5
= x²-6x+9-4
= x²-6x+3² -4
= (x-3)² -4
= (x-3)² - 2²

--> forme a² - b² : [(x-3)+2][(x-3)-2]
= (x+1) (x-5)

Il me semble que je m'en sors bien ! Merci !

[chan79]

Merci du coup je trouve

x²-6x+5
= x²-6x+9-4
= x²-6x+3² -4
= (x-3)² -4
= (x-3)² - 2²

--> forme a² - b² : [(x-3)+2][(x-3)-2]
= (x+1) (x-5)

Il me semble que je m'en sors bien ! Merci !

revois le calcul, c'est "presque" juste

[Agathe-72]

revois le calcul, c'est "presque" juste

Oui je viens de me rendre compte que ca n'allait pas en verifiant à la calculette, j'ai beau chercher je ne trouve pas où ... C'est une histoire de signe ?

[chan79]

Oui je viens de me rendre compte que ca n'allait pas en verifiant à la calculette, j'ai beau chercher je ne trouve pas où ... C'est une histoire de signe ?

x-3+2 est égal à x-1