Exprimer en fonction de
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 19 Avr 2007, 14:40
par Anonyme » 19 Avr 2007, 14:40
Bonjour, j'ai du mal à exprimer c en fonction de R
(c+(R/2))²-(5/4)R²=0
Merci d²vance de votre aide!
-
Matthy
- Membre Naturel
- Messages: 64
- Enregistré le: 04 Jan 2006, 01:05
-
 par Matthy » 19 Avr 2007, 14:42
par Matthy » 19 Avr 2007, 14:42
Salut,
c=(5/4)R²-(R/2))² puis tu developpes.
Bonne chance
-
Matthy
- Membre Naturel
- Messages: 64
- Enregistré le: 04 Jan 2006, 01:05
-
 par Matthy » 19 Avr 2007, 14:46
par Matthy » 19 Avr 2007, 14:46
Deso, j'avais mal vu les parenthses, donc voila:
c^2 + cR + (R/2)^2 -5R^2/4 = 0
Tu n'as plus qu'a simplifier.
Tu dois trouver C^2 + CR + R^2=0
cela revient a une equation de la forme: ax^2 + bx + c = 0
Tu calcules le discriminant et tu as ton resultat.
Bon courage
-
Anonyme
 par Anonyme » 19 Avr 2007, 14:57
par Anonyme » 19 Avr 2007, 14:57
discriminant ? qu'est ce que c'est? (j'ai jamais appris ça)
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 14:58
par allomomo » 19 Avr 2007, 14:58
Salut,
Soit :
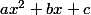
Discriminant :
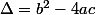
-
Anonyme
 par Anonyme » 19 Avr 2007, 15:04
par Anonyme » 19 Avr 2007, 15:04
allomomo a écrit:Salut,
Soit :
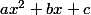
Discriminant :
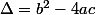
euh... j'ai peut etre oublié de dire que je suis en 2nde alors je ne sais pas si on apprend ça en 2nde
Tu dois trouver C^2 + CR + R^2=0
c'est c²+cR-R²=0 ?
je ne vois toujours pas comment exprimer c en fonction de R :triste:
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 15:07
par allomomo » 19 Avr 2007, 15:07
Re -
Ah, et bien il ne fallait pas oublier ... lol
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 15:09
par allomomo » 19 Avr 2007, 15:09
Salut,
Utilise l'identité remarquable suivante :
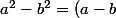(a+b))
Tu as
^2-\Big(\frac{\sqrt{5}}{2} R \Big)^2=\Big[\Big(\Big(c+\frac{R}{2}\Big)-\frac{\sqrt{5}}{2}R\Big) \Big]\Big[\Big(\Big(c+\frac{R}{2}\Big)+\frac{\sqrt{5}}{2}R \Big)\Big]=\Big(c+\frac{1-\sqrt{5}}{2}R\Big)\Big(c+\frac{1+\sqrt{5}}{2} R\Big)=0)
Donc
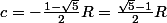
ou


est le nombre d'or.
-
Matthy
- Membre Naturel
- Messages: 64
- Enregistré le: 04 Jan 2006, 01:05
-
 par Matthy » 19 Avr 2007, 15:15
par Matthy » 19 Avr 2007, 15:15
123 a écrit:c'est c²+cR-R²=0 ?
excuse mon erreure... :we:
-
Anonyme
 par Anonyme » 19 Avr 2007, 15:28
par Anonyme » 19 Avr 2007, 15:28
Salut,
Utilise l'identité remarquable suivante :
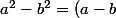(a+b))
Tu as
^2-\Big(\frac{\sqrt{5}}{2} R \Big)^2=\Big[\Big(\Big(c+\frac{R}{2}\Big)-\frac{\sqrt{5}}{2}R\Big) \Big]\Big[\Big(\Big(c+\frac{R}{2}\Big)+\frac{\sqrt{5}}{2}R \Big)\Big]=\Big(c+\frac{1-\sqrt{5}}{2}R\Big)\Big(c+\frac{1+\sqrt{5}}{2} R\Big)=0)
Merci!
mais comment avez vous fait pour passer de
-((V5/2)R))
en
/2)R)
??
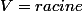
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 15:53
par allomomo » 19 Avr 2007, 15:53
Re -
x)
tu peux remplacer pour te convaincre :

et
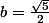
voila.
-
Anonyme
 par Anonyme » 19 Avr 2007, 16:12
par Anonyme » 19 Avr 2007, 16:12
ah d'accord merci beaucoup allomomo!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
