Expression de suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 25 Oct 2005, 08:51
par Anonyme » 25 Oct 2005, 08:51
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 25 Oct 2005, 12:34
par becirj » 25 Oct 2005, 12:34
Bonjour
Il faut savoir que avec x>0,
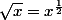
.

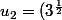^{1\over 2}=3^{1\over 4})
...
Une petite démonstration par récurrence s'impose
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 25 Oct 2005, 12:59
par rene38 » 25 Oct 2005, 12:59
Bonjour
moi, je trouve :




d'où la conjecture qu'il reste à démontrer :

c'est à dire

-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 25 Oct 2005, 13:04
par becirj » 25 Oct 2005, 13:04
Toutes mes excuses, j'ai effectivement oublié le 3 sous le radical.
-
Anonyme
 par Anonyme » 25 Oct 2005, 21:14
par Anonyme » 25 Oct 2005, 21:14
Merci beaucoup! Une dernière chose: comment procéder pour étudier le sens de variation de cette suite, ainsi que sa nature?
-
Anonyme
 par Anonyme » 25 Oct 2005, 21:44
par Anonyme » 25 Oct 2005, 21:44
De plus, en ce qui concerne la preuve par récurrence, il faut que je montre que la propriété est vraie au rang

, soit
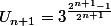
... cela me paraît... "évident" étant donné que l'on suppose que
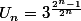
!
Comment procéder?
-
danskala
- Membre Relatif
- Messages: 129
- Enregistré le: 06 Mai 2005, 16:48
-
 par danskala » 25 Oct 2005, 22:31
par danskala » 25 Oct 2005, 22:31
salut,
on suppose que
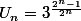
On a
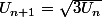
par définition de la suite Un
Donc
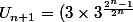^{\frac{1}{2}})
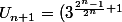^{\frac{1}{2}})
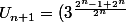^{\frac{1}{2}})
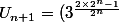 ^{\frac{1}{2}})
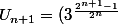^{\frac{1}{2}})
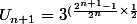})

cqfd
Bye
:we:
-
Anonyme
 par Anonyme » 25 Oct 2005, 23:06
par Anonyme » 25 Oct 2005, 23:06
Merci beaucoup!
Quant au sens de variation de la suite, si j'étudie l'exposant, comment en déduire le sens de variation?
De plus, comment montrer la nature de cette suite (converge ou diverge)?
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 26 Oct 2005, 02:30
par rene38 » 26 Oct 2005, 02:30
Comparons les exposants :

donc

(croissance de la fonction puissance sur IR +)
la suite est donc croissante.
--------------------------------------------

Le deuxième terme tend vers 0 lorsque n tend vers l'infini.

tend alors vers 3 ;

est donc convergente.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités