Exponentielles

[Elwyn]

Bonjour voila l'enoncé ( j'ai deja reussis le debut)

f(x) = x + 1 - e^(x / x+1 )

1) Reussi

2) a) Calculer f'(x) et f''(x)

f''(x) = (2x+1) / (x+1)² * e^(x/ x+1)

En deduire le sens de variation de f'

b) Dresser le tableau de variation de f' ( on admet lim en -1 f' = lim en +oo f' = 1)

3) Demontrer que f'x) = 0 admet sur ]-1,+oo[ 2 solution dont l'une est 0. Dans la suite du probleme on notera ALPHA la solution non nulle. Donner une valeur approchée de ALPHA.

4) Tableau de f.

Merci !

[Elsa_toup]

Bonsoir,

Je ne trouve pas le même f '(x) que toi. D'autant que 1-(x²-1) = -x²....
Y aurait-il un souci dans tes parenthèses ?

Je trouve f '(x) = 1 + * exp()

[Elwyn]

Je trouve pas mon erreur peux tu m'aider en detaillant svp ? de meme pour f'' car elle depend de f' donc j'ai forcement faux :hum:

de plus tu trouves 1 - or la fonction f c'est x + 1 - e ... non ?
c'est la dévrivée de l'exp qui pose probleme

[rene38]

Salut

Moi, je trouve

[Elsa_toup]

OK.

Alors la dérivée de x c'est 1. Celle de 1 c'est 0.
Donc on ne s'occupe que de exp().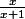

C'est de la forme exp(u(x)), donc la dérivée est : A = u'(x) * exp '(u(x)).
Or (exp)' = exp, donc on obtient:
u'(x) * exp(u(x)).

u(x) est de la forme v(x)/w(x), donc u'(x) = [v'(x)*w(x) - v(x)*w'(x)]/w²(x).

v(x) = x, et w(x) = x+1.
Donc u'(x) = [(x+1)-x]/(x+1)² = 1/(x+1)²

Donc A = exp(x/x+1) * 1/(x+1)².

Donc f '(x) = 1 - A.

P.S: oui, je m'étais trompée avant ... :ptdr: Mais bon là je suis sûre.
C'est bon, c'est clair ?

[Elwyn]

Ah vous trouvez pas pareil :doh: De plus rené regarde on me donne f'' plus loin dans l'exercice et c'est pas ca ... bizarre

[Elwyn]

C'est bon j'ai compris ! lol
mais pas pour f'', y a des termes de partout et j'ai pas encore le reflexe simplifier du prof ^^

[Elwyn]

Quelqu'un peut m'aider ? Quelqu'un qui dort pas lol

[Elsa_toup]

Bon, là tu dérives un truc de la forme -u*v, donc la dérivée est -(u'v+uv'), avec u(x) = 1/(x+1)², et v(x) = exp(x/x+1)

Donc u'(x) = -2/, et v'(x) = A (celui de tout à l'heure).

On obtient donc: f ''(x) = - [-2exp((x/x+1)/ + A/(x+1)²]

Je rappelle que A = exp(x/x+1) * 1/(x+1)².

Donc f ''(x) = - exp(x/x+1) [-2/ + 1/] = -exp(x/x+1) [ (1-(2x+2))/ ] = (2x+1)*exp(x/x+1)/

[Elwyn]

Merci ! Mais on me donne f'' plus loin et c'est pas tout a fait ca ( c'est ... sur (x+1)²)

On me dit : Verifier que ... je pense que ca veut dire trouvez ca, mais pourquoi me demanderez t ils de calculer f'' alors ?

[Elsa_toup]

Non, c'est sur .
Ensuite pour le sens de variation de f '(c), tu étudies le signe de f ''(x).

[Elwyn]

Pourquoi me demande t ils de verifier si f''(x) = (2x+1 / x+1)² * exp(x/x+1)

En bref le signe de f'' depend de 2x+1 on a donc

-1 ______________ - 1/ 2 _______________ +oo

f'' _______ - _________ 0 _______ + _______

f'' decroissante _____________ croissante

non ?

[rene38]

A peu près : f ' et non f '' sur la dernière ligne.

[Elwyn]

Merci !

On me demande maintenant ca :

3) Demontrer que f'x) = 0 admet sur ]-1,+oo[ 2 solution dont l'une est 0. Dans la suite du probleme on notera ALPHA la solution non nulle. Donner une valeur approchée de ALPHA.
J'imaine qu'il faut utiliser le theoreme des valeurs intermédiaires non ?

[rene38]

Absolument -après en avoir vérifié les hypothèses.

[Elwyn]

Je dis que f' est monotone sur 1 , -1/2 , de plus f'(-1) > 0 et f'(1-4/e) < 0 ,donc d'apres le theoreme l'equation f'(x) = 0 a une solution sur I = ]-1 , 1- 4/e [

De meme pour -1/2 , +oo

C'est ca ?

[rene38]

Je dis que f' est monotone sur -1 , -1/2 ,
de plus f'(-1) > 0 et f'(1-4/e) < 0 non : f '(-1/2)=1-4/e<0,
donc d'apres le theoreme l'equation
f'(x) = 0 a une solution sur I = ]-1 , 1- 4/e [ non : sur ]-1 ; -1/2]

De meme pour -1/2 , +oo(***)

C'est ca ?

(***) mais cette solution est évidente : c'est 0

[Elwyn]

Merci ! j'ai galérer la lol
Pour la valeur approchée j'ai mis :

f'(-3.1) < f'(a) < f'(-3)
donc -3.1 < a < -3

je dois maintenant etudier les ariations de f :

1) limites aux bornes (je devaris y arriver)
2) Tableau de variation (je vais essayer)

je reviens si probleme

[Elwyn]

Je trouve lim -1 = - oo
lim +oo = +oo

Tableau :

x | -1 _______ A _______ 0 _________ +oo

f | croit | decroit | croit

mais alpha je trouve environs -3 et c'est pas logique (plus haut)

[Elwyn]

Aidez moi svp :)

PS : je dois aussi trouver la limite de (x/x+1) * exp(x/x+1) or c'est une forme indéterminée mais je sais pas comment factoriser