Exercice Thalès seconde

[lazyboy244]

Bonjour
Je suis un étudiant et je donne des cours de soutien en mathématiques. L'autre jour g rencontré un exercice avec une élève que g en seconde. voici l'énoncé :

Un verre rempli d'eau est schématisé par un triangle ABC de hauteur CH. Le niveau d'eau est représenté par le segment [PQ] (Voir schéma)

Etudier les 2 interprétations possibles de : "Le verre est à moitié plein"

Schéma

[lazyboy244]

ça m'a pris de court. Je ne suis jamais tombé sur un exercice pareil.
J'ai pensé :

* Interpretation surfacique : Aire(CPQ) = Aire (ABPQ)

* Interpretation volumique : Volume du cône de sommet C et de base le cercle de diamètre [PQ] = Volume du tronc de cône ayant les 2 bases le cercle de diamètre [PQ] et celui de diamètre [AB].

On utilisera thalès pour établir une relation entre les 2 hauteurs [CH] et [CM] puis on cherchera la valeur de CM pour les deux interpretation.

Est-ce que c'est la solution? où y a-t-il une autre interpretation à laquelle je n'ai pas pensé?

Merci

[laya]

* Interpretation surfacique : Aire(CPQ) = Aire (ABPQ)

* Interpretation volumique : Volume du cône de sommet C et de base le cercle de diamètre [PQ] = Volume du tronc de cône ayant les 2 bases le cercle de diamètre [PQ] et celui de diamètre [AB]

Merci

Euh, l'aire de CPQ ne peut pas être égale à celle de ABPQ, le seul cas où cela peut arriver est lorsque C=P=Q (ABPQ n'est alors plus un quadrilatère).
Les triangles CBA et CPQ sont semblables. Soit k leur rapport de "semblabilité", k>1, le rapport des aires de CBA et CPQ est alors k² (et non pas k).
Pour que le verre soit à moitié plein, il faut et il suffit que k²=2, c'est-à-dire .

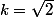
[lazyboy244]

et du coup pour la deuxième interpretation on di que le volume du petit cône doit faire la moitié du grand cone du coup [TEX ]k^3=2[/TEX]

[laya]

et du coup pour la deuxième interpretation on di que le volume du petit cône doit faire la moitié du grand cone du coup [TEX ]k^3=2[/TEX]

Oui, ce qu'on peut justifier en écrivant : CA = k CP, CB = k CQ et AB = k PQ.