Bonjour,
voilà la question:
une boite sans couvercle de contenance 0,5L, a la forme d'un pavé droit de base carrée de coté x cm et de hauteur h cm.
1a- justifier que x^2*h=500
b- en déduire que l'aire extérieure de la boite (fond plus parois latérales) est, pour tout x € ]0;+infini[ :
A(x)=x^2 + (2000/x)
2- trouver les dimensions de la boite pour lesquelles l'aire extérieure est minimale et préciser cette aire.
si quelqu'un sais répondre à une de ces questions ça m'aidera beaucoup, merci d'avance!
Exercice maths 1er application de la dérivation
8 messages
- Page 1 sur 1
Re: exercice maths 1er application de la dérivation
Bonsoir,
Pour t'aider à débuter comme je ne sais pas où tu en es, n’hésite pas à le préciser une prochaine fois, ce sera plus facile pour te guider
1a) L'aire d'un carré est : coté x coté
Le volume d'un pavé droit est : aire du fond x hauteur
1b) Il faut sommer l'aire du fond qui a déjà été calculée avec l'aire des parois latérales qui sont des rectangles,
il y a 4 parois en tout (pour mémoire l'aire d'un rectangle est : largeur x longueur).
De plus à partir de la question précédente tu peux exprimer h en fonction de x
2) Maintenant qu'on connait une formule pour l'aire extérieure qui est une fonction de x, comment faire pour trouver son minimum ? Autrement dit comment faire pour étudier le sens de variation d'une fonction ?
Indice : le titre de l'exercice
Pour t'aider à débuter comme je ne sais pas où tu en es, n’hésite pas à le préciser une prochaine fois, ce sera plus facile pour te guider
1a) L'aire d'un carré est : coté x coté
Le volume d'un pavé droit est : aire du fond x hauteur
1b) Il faut sommer l'aire du fond qui a déjà été calculée avec l'aire des parois latérales qui sont des rectangles,
il y a 4 parois en tout (pour mémoire l'aire d'un rectangle est : largeur x longueur).
De plus à partir de la question précédente tu peux exprimer h en fonction de x
2) Maintenant qu'on connait une formule pour l'aire extérieure qui est une fonction de x, comment faire pour trouver son minimum ? Autrement dit comment faire pour étudier le sens de variation d'une fonction ?
Indice : le titre de l'exercice
Re: exercice maths 1er application de la dérivation
Bonsoir,
Merci beaucoup pour votre réponse mais je n'arrive pas à trouver les variations. Après avoir dérivé A je trouve 2x-2000 ce qui me donne une tableau de variation bizarre, le minimum est atteint pour x=1000 qui vaut 1000002. J'ai aussi essayé (2(x^3-1000))/x^2 car mon prof nous a dit qu'on doit trouver x^3-1000 au numérateur mais j'arrive pas à faire un tableau de variation avec ça.
Merci beaucoup pour votre réponse mais je n'arrive pas à trouver les variations. Après avoir dérivé A je trouve 2x-2000 ce qui me donne une tableau de variation bizarre, le minimum est atteint pour x=1000 qui vaut 1000002. J'ai aussi essayé (2(x^3-1000))/x^2 car mon prof nous a dit qu'on doit trouver x^3-1000 au numérateur mais j'arrive pas à faire un tableau de variation avec ça.
Re: exercice maths 1er application de la dérivation
Bonsoir,
Je pense qu'il y a une petite erreur dans la dérivée, il faut dériver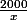 et cela ne donne pas 2000. Que vaut la dérivée de
et cela ne donne pas 2000. Que vaut la dérivée de  ?
?
Je pense qu'il y a une petite erreur dans la dérivée, il faut dériver
Re: exercice maths 1er application de la dérivation
1/x dérivée = -1/x^2 donc 2000/x dérivée = -2000/x^2
mais ça change pas mes calcules :c
mais ça change pas mes calcules :c
Re: exercice maths 1er application de la dérivation
Voilà, c'est beaucoup mieux du coup la dérivée vaut donc 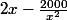
Ensuite il ne reste plus qu'à mettre au même dénominateur est étudier la (ou les) valeur(s) qui annule(nt) la dérivée.
Pour quelle valeur de le numérateur va valoir 0 ?
le numérateur va valoir 0 ?
Ensuite il ne reste plus qu'à mettre au même dénominateur est étudier la (ou les) valeur(s) qui annule(nt) la dérivée.
Pour quelle valeur de
Re: exercice maths 1er application de la dérivation
Avec plaisir, je n'ai fais que te poser des questions donc bravo à toi pour avoir réussi l'exercice 
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
