Exercice 2nde sur les vecteurs
15 messages
- Page 1 sur 1
Exercice 2nde sur les vecteurs
Bonjour à tous !
Alors voilà je suis bloquée à cet exercice, pour la question 1), j'ai trouvé D(1;-3) est-ce bon ? Pour la question 2), je ne suis vraiment pas sûre de mon raisonnement mais j'ai E(-7/2 ; 9/2). Je bloque à la question 3), mais pour la 4) j'ai raisonné à partir de mes résultats précédents donc ça me parait faux, j'ai F(16;0). Les dernières questions sont celles où je bloque totalement ... pourriez vous m'aider s'il vous plaît ?
(je place un 'v' pour signaler un vecteur, ne sachant pas où se trouve la flèche des vecteurs ^^')
1) Placer dans un repère (O;vi;vj) les points A(-2;4), B(3;5) et C(6;-2).
Déterminer les coordonnées du point D tel que ABCD parallélogramme et placer le point D.
2) Soit E point défini par vED-3vEA=v0
Calculer les coordonnées du point E, puis le placer sur la figure.
3) Démontrer que vAE = 1/2vDA
4 Calculer les coordonnées du point défini par vCF=2vDC. Placer le point F.
5) Démontrer que les points E, F et B sont alignés. (j'ai déjà résolu cette question)
6) K est le milieu de [CF] ; L est le milieu de [BC].
Démontrer que L est le milieu de [AK].
Merci d'avance pour votre aide ! :jap:
Alors voilà je suis bloquée à cet exercice, pour la question 1), j'ai trouvé D(1;-3) est-ce bon ? Pour la question 2), je ne suis vraiment pas sûre de mon raisonnement mais j'ai E(-7/2 ; 9/2). Je bloque à la question 3), mais pour la 4) j'ai raisonné à partir de mes résultats précédents donc ça me parait faux, j'ai F(16;0). Les dernières questions sont celles où je bloque totalement ... pourriez vous m'aider s'il vous plaît ?
(je place un 'v' pour signaler un vecteur, ne sachant pas où se trouve la flèche des vecteurs ^^')
1) Placer dans un repère (O;vi;vj) les points A(-2;4), B(3;5) et C(6;-2).
Déterminer les coordonnées du point D tel que ABCD parallélogramme et placer le point D.
2) Soit E point défini par vED-3vEA=v0
Calculer les coordonnées du point E, puis le placer sur la figure.
3) Démontrer que vAE = 1/2vDA
4 Calculer les coordonnées du point défini par vCF=2vDC. Placer le point F.
5) Démontrer que les points E, F et B sont alignés. (j'ai déjà résolu cette question)
6) K est le milieu de [CF] ; L est le milieu de [BC].
Démontrer que L est le milieu de [AK].
Merci d'avance pour votre aide ! :jap:
Bonjour,
1) Comment trouves-tu ton point D ? Peux-tu détailler ton calcul car je ne trouve pas la même chose que toi
2) On va déjà vérifier que ton point D est le bon
3) Si ton point D est faux, il est normal que tu ne trouves pas le résultat
4) Idem
5) Il suffit de montrer que EF et EB sont colinéaires EF = k EB (k à déterminer)
6) Tu calcules les coordonnées de K et L et tu vérifies que tu as bien


1) Comment trouves-tu ton point D ? Peux-tu détailler ton calcul car je ne trouve pas la même chose que toi
2) On va déjà vérifier que ton point D est le bon
3) Si ton point D est faux, il est normal que tu ne trouves pas le résultat
4) Idem
5) Il suffit de montrer que EF et EB sont colinéaires EF = k EB (k à déterminer)
6) Tu calcules les coordonnées de K et L et tu vérifies que tu as bien
ampholyte a écrit:Bonjour,
1) Comment trouves-tu ton point D ? Peux-tu détailler ton calcul car je ne trouve pas la même chose que toi
2) On va déjà vérifier que ton point D est le bon
3) Si ton point D est faux, il est normal que tu ne trouves pas le résultat
4) Idem
5) Il suffit de montrer que EF et EB sont colinéaires EF = k EB (k à déterminer)
6) Tu calcules les coordonnées de K et L et tu vérifies que tu as bien
1) J'ai fait vAB(5;1)
vDC(6-x;-2-y)
donc 5 = 6-x
1= -2-y ceci équivaut donc à x=1 et y=-3
voila ! :happy2: (merci de bien vouloir m'aider ! :jap: )
Bon, repartons du début.
On a : A(-2;4), B(3;5) et C(6;-2)
1) On cherche D(x, y) tel que
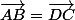
 = (3 +2; 5 - 4) = (5; 1))
 = (6 - x; -2 - y))
D'où :
 donc
donc 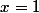
 donc
donc 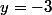
D(1; -3) => On est d'accord.
2) On a A(-2;4), B(3;5), C(6;-2) et D(1; -3)
On cherche E(x, y) tel que

 = (1 - x; -3 - y))
 = (-2 - x; 4 - y))
D'où
 - 3(-2 - x) = 0) donc
donc 
donc
 - 3(4 - y) = 0) donc
donc 
donc
E(7/2; 15/2)
3) On a donc A(-2;4), B(3;5), C(6;-2), D(1; -3) et E(-7/2; 15/2)
 = (-7/2 + 4/2; 15/2 - 8/2) = (-3/2; 7/2))
 = (1 + 2; -3 - 4) = (3; -7))
Es-tu sûre que l'expression n'est pas car dans ce cas ça fonctionne !
car dans ce cas ça fonctionne !
4) On a A(-2;4), B(3;5), C(6;-2), D(1; -3), E(-7/2; 15/2) et F(x,y)
vCF=2vDC
)
 = (5; 1))
D'où
 donc
donc 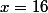
 donc
donc 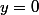
F(16; 0)
5) On calcule BF et BE
 = (13; -5))
 = (-13/2; 5/2))
On a donc

Les vecteurs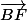 et
et 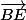 étant colinéaire alors B, E et F sont alignées.
étant colinéaire alors B, E et F sont alignées.
6)On a A(-2;4), B(3;5), C(6;-2), D(1; -3), E(-7/2; 15/2) et F(16,0)
K est le milieu de [CF], donc
)
K(11; -1)
L est le milieu de [BC]
)
L(9/2; 3/2)
Si L milieu de AK alors
)
L(9/2; 3/2)
Fin du problème OUF !!
Si tu as des questions n'hésite pas .
.
On a : A(-2;4), B(3;5) et C(6;-2)
1) On cherche D(x, y) tel que
D'où :
D(1; -3) => On est d'accord.
2) On a A(-2;4), B(3;5), C(6;-2) et D(1; -3)
On cherche E(x, y) tel que
D'où
donc
donc
E(7/2; 15/2)
3) On a donc A(-2;4), B(3;5), C(6;-2), D(1; -3) et E(-7/2; 15/2)
Es-tu sûre que l'expression n'est pas
4) On a A(-2;4), B(3;5), C(6;-2), D(1; -3), E(-7/2; 15/2) et F(x,y)
vCF=2vDC
D'où
F(16; 0)
5) On calcule BF et BE
On a donc
Les vecteurs
6)On a A(-2;4), B(3;5), C(6;-2), D(1; -3), E(-7/2; 15/2) et F(16,0)
K est le milieu de [CF], donc
K(11; -1)
L est le milieu de [BC]
L(9/2; 3/2)
Si L milieu de AK alors
L(9/2; 3/2)
Fin du problème OUF !!
Si tu as des questions n'hésite pas
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
