évaluation limite

[mathnul]

Bonjour, voilà une journée que je me démerde à tenter de trouver une solution à ce problème.

Évaluez. si elle existe, la limite suivante: limite si x tend vers inf de: x^2-ln(x^2+1) . Voilà, j'essai de le mettre en forme 0/0 ou inf/inf pour appliquer la formule de l'hospital en multipliant les deux cotés par x et les divisant de x du même coup sauf que cela ne m'avance pas plus loin.... Auriez-vous une idée comment régler ce problème?

[Lostounet]

Bonjour, voilà une journée que je me démerde à tenter de trouver une solution à ce problème.

Évaluez. si elle existe, la limite suivante: limite si x tend vers inf de: x^2-ln(x^2+1) . Voilà, j'essai de le mettre en forme 0/0 ou inf/inf pour appliquer la formule de l'hospital en multipliant les deux cotés par x et les divisant de x du même coup sauf que cela ne m'avance pas plus loin.... Auriez-vous une idée comment régler ce problème?

Bonsoir,
Puisque c'est une indétermination de la forme "+infini" - "+infini", il faut essayer de voir lequel des "infini" l'emporte. La méthode qui vient à l'esprit est la factorisation par le terme dominant, et on se doute que c'est "x^2" vu que ln(x^2 + 1) "agit comme" ln(x^2) donc 2ln(x) qui croit assez lentement. Pour mettre tout cela en forme:

Par exemple:







Qui tend vers + l'infini par produit des limites et continuité du logarithme en 1, et par le fait que ln(x)/x^2 tend vers 0 (croissances comparées)

[Lostounet]

Autre méthode:

Posons alors:
positive pour tout x>0, donc la fonction g est convexe (sur 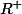) et sa courbe est en particulier au dessus de sa tangente en x = 1. Cette tangente a pour équation

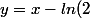Nous en déduisons, pour tout x>0, et nous concluons par minoration.