Etudier le signe de ..

[Furi0u5]

Jour !

Un truc de seconde...

Si je dois étudier le signe de f(x) - g(x), je dois faire quoi encore? ^^
Tableau de signe?
Ou juste calculer f(x) - g(x) ?
:/

Merci, bon dimanche

[Furi0u5]

eupe :hein:

[math*]

Tu calcules f(x) - g(x) et tu étudies le signe de ce que tu trouves.

[Furi0u5]

L'équation 2x² + 2 = 0 n'a pas de solutions
Donc je dois mettre les deux barres non ? :hum:

[Elsa_toup]

Bonjour,

Tu veux pas nous mettre tout l'énoncé ?
Je comprends rien là ... lol :we:

[Kerdy]

Perso, j'ai trouvé un résultat négatif pour ce DM mais je sais pas comment linterpreter.

[Furi0u5]

Ouais c'est vrai lol ^^

Ma fonction: f(x) =

Je l'ai dérivée. Ca donne:


Je devais déterminer l'équation réduite de la tangente T à la courbe en 0.
J'ai trouvé: y =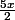

Puis là je dois étudier le signe de f(x) - g(x) avec g la fonction dont la tangente T est la représentation graphique.

Alors je trouve: f(x) - g(x) =

Et après? Tableau de signe? Comment? 2x² + 2 = 0 est impossible alors je fais quoi ?

Kerdy qu'est ce que t'apelles résultats négatif? C'est négatif ou ? :hum:

[Kerdy]

Je met l'énoncé pour que les autres comprennent:


Pour le résultat de f(x)-g(x), j'ai trouvé un résultat négatif.

[Elsa_toup]

Ah, c'est quand même mieux avec un énoncé ! lol
Mais je trouve pas comme toi pour la dérivée ...
J'ai f '(x) = .

Qu'en penses-tu ???

[Furi0u5]

Euh.. je sais pas
Je pense que ma dérivée est juste.
Kerdy t'as trouvé quoi comme dérivée?

[Kerdy]

Pareil que toi sauf que j'ai pas développé le dénominateur (comme le prof nous a dit).

[Elsa_toup]

Ben je voudrais pas paraître négative ( :hum: )à, mais je pense que c'est faux.
La dérivée de u/v est (u'v-uv')/v²....

[Kerdy]

C'est ce que j'ai fait. :hum:

[Elsa_toup]

lol, ben alors t'as pas pu trouver comme Furious05.
Sa plus grande puissance au dénominateur c'est .
Il devrait avoir des trucs en et ...

[Kerdy]

Effectivement, le dénominateur de la dérivée qu'a trouvé Furious est faux car le dénominateur non développé est: (2x²+2)²
Ce qui donne après développement: 4x4+8x²+4.

[Elsa_toup]

Ok, ben là je suis d'accord alors, mais au numérateuir, j'ai pas 10 moi, j'ai 5....

Toujours est-il que l'équation de la tangente en x=0, est donnée par y = f '(0)(x-0)+f(0) = (5/2) x + 0.
Donc y=5x/2.

g(x) = 5x/2.

Donc .

C'est 0 et > 0 pour x 0, c'est du signe de -)

[Furi0u5]

(je viens de voir que c'est ce que Furious05 avait trouvé, donc c'est nickel. Il suffit de dire que, comme le dénominateur est toujours > 0, c'est du signe de -5x^3

:we: :we: :we: :we: :we: :we:

C'est 0 et > 0 pour x < 0.

C'est la réponse à la question ? Suffit de dire ça? Besoin de faire un tableau de signe?

Merci à toi Elsa_Top de toutes tes réponses

[Elsa_toup]

Ben c'est pas franchement la peine.
Si tu fais un tableau de signes, tu auras une ligne avec le dénominateur, qui est toujours positif (donc des + partout), et une ligne avec le numérateur, qui est, comme je l'ai écrit plus haut, positif jusqu'en 0, puis négatif.

Donc, non, ce n'est pas nécessaire.

P.S: pas de quoi ! :we:
(en fait, j'ai mis 3 h, mais t'avais presque tout fait...)

[Furi0u5]

Merciiiiii ok!!!
3 Heures????
Pour perdre ton temps avec des incapables comme nous? :p :p

Nah c'est très gentil :)

Et encore un dernier dernier truc lol
En déduire la position de C par rapport à delta.
Faut dire quoi ?
Position = au dessus ou en dessous?

:++:

[Elsa_toup]

Oui, c'est ça.
Quand f(x)-g(x) > 0, f(x) > g(x), donc C est au-dessus de .
Et inversement pour négatif.

Bonne soirée ! :happy2: