étudier le signe de f'(x)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 11 Oct 2008, 18:39
par guigui51250 » 11 Oct 2008, 18:39
Salut tout le monde
Dans un de mes exo je rencontre un problème.
Sur
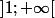
,
=x+1+\frac{x}{x^2-1})
donc
=1+\frac{-x^2-1}{(x^2-1)^2})
je dois déterminer le signe de
)
pour ensuite voir les variations de

voilà ce que j'ai fait :
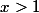
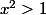

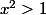
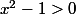
^2>0)
après je bloque, je n'arrive pas à en conclure le signe de
)
Quelqu'un pourrait m'expliquer comment faire svp?
-
rain
- Membre Relatif
- Messages: 142
- Enregistré le: 05 Oct 2008, 12:11
-
 par rain » 11 Oct 2008, 18:47
par rain » 11 Oct 2008, 18:47
f'(x)>=0 <=> x(x-3)>=0
donc f décroissante sur [0,3].
Si tu comprends pas tout demande j'te donnerai les détails des calcules.
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 11 Oct 2008, 18:50
par guigui51250 » 11 Oct 2008, 18:50
rain a écrit:f'(x)>=0 x(x-3)>=0
donc f décroissante sur [0,3].
Si tu comprends pas tout demande j'te donnerai les détails des calcules.
et pourquoi? je n'ai pas compris ton raisonnement :hum:
-
Equiangle
- Membre Naturel
- Messages: 97
- Enregistré le: 09 Oct 2008, 12:56
-
 par Equiangle » 11 Oct 2008, 18:53
par Equiangle » 11 Oct 2008, 18:53
rain a écrit:f'(x)>=0 x(x-3)>=0
donc f décroissante sur [0,3].
Si tu comprends pas tout demande j'te donnerai les détails des calcules.
Je pense que tu as du te tromper dans tes calculs...Ce n'est pas ça. f'(3) n'est pas nul donc ça ne va pas!
-
rain
- Membre Relatif
- Messages: 142
- Enregistré le: 05 Oct 2008, 12:11
-
 par rain » 11 Oct 2008, 18:54
par rain » 11 Oct 2008, 18:54
f'(x)>=0 <=> 1>=(x²+1)/(x²-1)² <=> (x-1)²>=x²+1
Ensuite tu devellopes, tu mets tout du même coté et t'obtient :
x^4-3x²>=O <=> x(x-3)>=0, OK?
-
Equiangle
- Membre Naturel
- Messages: 97
- Enregistré le: 09 Oct 2008, 12:56
-
 par Equiangle » 11 Oct 2008, 18:56
par Equiangle » 11 Oct 2008, 18:56
guigui51250,
Pour connaitre les variations de f(x), donc le signe de f'(x) moi j'aurais plutôt essayé de mettre f'(x) sous forme d'un produit de facteur. f'(x)=A*B/C² donc après il est simple d'étudier le signe de A et de B.(C² étant positif).
-
rain
- Membre Relatif
- Messages: 142
- Enregistré le: 05 Oct 2008, 12:11
-
 par rain » 11 Oct 2008, 18:57
par rain » 11 Oct 2008, 18:57
Euh oui merci j'ai fait une erreur mais la marche à suivre est la même, et les racines c'est + et - racine de 3 .
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 11 Oct 2008, 18:58
par guigui51250 » 11 Oct 2008, 18:58
ok je vais essayer de faire comme ça
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 11 Oct 2008, 19:02
par guigui51250 » 11 Oct 2008, 19:02
ah c'est bon j'ai trouvé, merci pour vos conseils :we:
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 11 Oct 2008, 19:47
par guigui51250 » 11 Oct 2008, 19:47
Equiangle a écrit:guigui51250,
Pour connaitre les variations de f(x), donc le signe de f'(x) moi j'aurais plutôt essayé de mettre f'(x) sous forme d'un produit de facteur. f'(x)=A*B/C² donc après il est simple d'étudier le signe de A et de B.(C² étant positif).
avec cet méthode je trouve f'(x) négatif sur 1;racine de 2 et positif sur racine de 2;+ l'infini
et j'ai vérifié c'est bon, merci pour l'explication :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités