Bonsoir, j'ai pratiquement terminée un DM sauf 2 équations sur 8 que j'ai pas compris, si quelqu'un pouvait m'expliquer ce serait sympas. Je met les réponses de deux équations dite moi si c'est juste ou pas.
1)(3x+4)au cube(2x+1)²(x-5)=0
regle du double produit:
3x+4=0 ::ou 2x+1=0 :: ou x-5=0
3x=-4 :: 2x=-1 :: ou x=5
x=-4/3 :: x=-1/2 ::
2)9x²-16+2(3x-4)(x+2)=(3x-4)²
pas compris
3)(2x-3/2)²=4(3x+1)²
pas compris
8)3x+2/x+2=2/x
produit en croix:
3x+2*x=x+2*2
5x=x+4
4x=4
x=1
équations, premier, deuxieme degré 2nde
5 messages
- Page 1 sur 1
2)9x²-16+2(3x-4)(x+2)=(3x-4)²
As tu déjà vu la résolution d'équation du second degré à l'aide du discriminant ?
L'idée c'est de mettre l'équation sous la forme ax²+bx+c = 0
9x²-16+2(3x-4)(x+2)=(3x-4)²
<=> 2)9x²-16+2(3x-4)(x+2) - (3x-4)² = 0
EN développant le membre de gauche tu devrais obtenir une équation de la bonne forme.
Même principe pour l'autre.
As tu déjà vu la résolution d'équation du second degré à l'aide du discriminant ?
L'idée c'est de mettre l'équation sous la forme ax²+bx+c = 0
9x²-16+2(3x-4)(x+2)=(3x-4)²
<=> 2)9x²-16+2(3x-4)(x+2) - (3x-4)² = 0
EN développant le membre de gauche tu devrais obtenir une équation de la bonne forme.
Même principe pour l'autre.
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
La solution "barbare" serait de tout mettre du même coté, de développer de calculer delta et les racines (tu as vu la résolution d'équation du second degré ?)
Je pense qu'il y a une solution plus élégante, je crois voir des identités remarquables tu type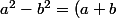(a-b)) notamment pour la 3 (passer tout du même coté avant)
notamment pour la 3 (passer tout du même coté avant)
Pour la 2 que tu devrais factoriser, y aura de la simplification à faire
que tu devrais factoriser, y aura de la simplification à faire
Je pense qu'il y a une solution plus élégante, je crois voir des identités remarquables tu type
Pour la 2
Jiiinkz a écrit:vous me proposé de technique différente vous deux laquelle est la meilleur ?
je n'ai vu que les équation du second degré, premier degré, identité remarquable et facteur commun.
je n'ai pas vu de discriminant ou de delta.
vous pouvez réexpliquer svp
Si tu n'as pas encore vu le discriminant tu dois faire comme dit plus haut et tenter de factoriser en te servant des identité remarquables.
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
