Equation d'une droite vectorielle...

[MacErmite]

Bonjour,

Je suis perdu dans les equations de droites, de plans... et j'aurais une petite question sur ce sujet; si une droite D à pour équations cartésiennes



est-ce juste de dire que sa droite vectorielle à pour equations



??

Merci

[Nightmare]

Salut,

je n'ai pas compris la question. "sa droite vectorielle" ? La droite vectorielle de qui?

[MacErmite]

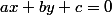
Par analogie dans , l'equation d'une droite est de la forme et j'ai sous les yeux l'équation de la droite vectorielle :
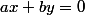
Apparement je suis dans l'erreur ?

[Nightmare]

Une droite vectorielle c'est juste une droite qui passe par l'origine donc si tu cherches une droite vectorielle parallèle à celle d'équation ax+by+c=0, on retrouve bien la droite d'équation ax+by=0.

[MacErmite]

Une droite vectorielle c'est juste une droite qui passe par l'origine donc si tu cherches une droite vectorielle parallèle à celle d'équation ax+by+c=0, on retrouve bien la droite d'équation ax+by=0.

Alors si je reprends le système représentant la droite D, énoncé plus haut, la droite passant par 0 et parallèle à cette droite à pour système d'équations :


??

[Ericovitchi]

oui ce sont bien 2 plans respectivement parallèles aux deux premiers et ils passent par l'origine donc ils décrivent bien une droite passant par l'origine et parallèle à la droite initiale (si c'est bien ce que tu cherchais).