Equation du troisième degrée - déterminer les racines
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 18 Oct 2020, 17:58
par novicemaths » 18 Oct 2020, 17:58
Bonsoir
J'ai
=m^3-7m+6)
Pour m=1 on a
=1^3-7 \times 1+6=1-7+6=0)
On voit que m=1 est une racine de p
p(m)=(m-1)q(m)
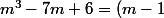(am^2+bm+c))
Je ne vois pas comment continuer, vu que mon équation de départ n'est pas complète.
Pourriez-vous me guider pour la suite?
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 18 Oct 2020, 18:01
par GaBuZoMeu » 18 Oct 2020, 18:01
novicemaths a écrit:Je ne vois pas comment continuer, vu que mon équation de départ n'est pas complète.
Bonsoir,
Et alors, en quoi ça gêne pour faire la division ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 18 Oct 2020, 18:16
par novicemaths » 18 Oct 2020, 18:16
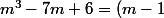(am^2+bm+c))
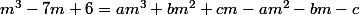
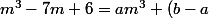m^2+(c-b)m-c)
Par indentification:
a=1
(b-a)=0
c-b=7
-c=6
Ce qui donne:
a=1
(-6-1)=-7
c=-6
Pour moi le résultat n'a pas de sens, car
(m^2 -7m-6))
Si on fait le calcul, le résultat ne correspond pas à l'équation de départ.
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 18 Oct 2020, 20:03
par Pisigma » 18 Oct 2020, 20:03
Bonsoir,
en factorisant dès le départ,
=m^3-7\,m+6)
=m^3-m-6\,m+6)
...
-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
 par Rdvn » 18 Oct 2020, 20:19
par Rdvn » 18 Oct 2020, 20:19
Bonsoir
@novicemaths
Votre méthode est correcte (c'est celle pratiquée usuellement en Terminale)
mais attention aux calculs :
c-b = -7 (et non 7)
Pour vérifier
Immédiat a=1, c= -6, en reportant dans les deux autres équations on trouve b=1 pour chacune
Bon courage
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 18 Oct 2020, 20:31
par novicemaths » 18 Oct 2020, 20:31
(m^2-7m-6)=m^3-7m^2-6m-m^2+7m+6=m^3-6m^2+m+6)
Mon soucis est que
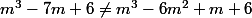
Je ne retrouve pas l'équation de départ, où ai-je fais erreur dans mon calcule?
A bientôt
-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
 par Rdvn » 18 Oct 2020, 20:37
par Rdvn » 18 Oct 2020, 20:37
Lisez vos messages ! Je viens de vous le dire juste ci dessus, dans mon message précédent !
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 18 Oct 2020, 21:28
par novicemaths » 18 Oct 2020, 21:28
Je récapitule -6-b=-7 <=>-b=-7+6 <=> -b=-1 <=>b=1
Erreur d'inattention

(m^2+m-6)=m^3+\not{m^2}-6m-\not{m^2}-m+6 = m^3-6m-m+6=m^2-7m+6)
Là! Ca va mieux.
Merci
A bientôt
-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
 par Rdvn » 18 Oct 2020, 21:41
par Rdvn » 18 Oct 2020, 21:41
Cette fois ci ça va .
Il y a aussi la vérification par la 2ème égalité
b-a = 0 ,
donc b = a = 1
Bonne nuit
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités