équation sur les exponentielles

[MARJORIE 35390]

Bonjour , j'ai une équation à résoudre avec des exponentielles mais je ne vois pas comment faire .. :/
C'est :

[ElWaner]

Salut,

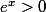
pour tout x réel. Donc ton équation peut se simplifier (division par un nombre strictement positif):

. C'est une équation du second degré que tu n'a plus qu'a résoudre pour trouver les racines qui seront les solutions!

[MARJORIE 35390]

Salut,

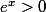
pour tout x réel. Donc ton équation peut se simplifier (division par un nombre strictement positif):

. C'est une équation du second degré que tu n'a plus qu'a résoudre pour trouver les racines qui seront les solutions!

le nombre on l'enlève pour résoudre l'équation ?

[ElWaner]

Oui c'est comme si tu avais une équation du type:

avec a > 0.
En divisant l'égalité à gauche et à droite par a
tu obtiens

Tu peux diviser à gauche et à droite par a car a est strictement positif (jamais égal à 0).

[MARJORIE 35390]

Oui c'est comme si tu avais une équation du type:

avec a > 0.
En divisant l'égalité à gauche et à droite par a
tu obtiens

Tu peux diviser à gauche et à droite par a car a est strictement positif (jamais égal à 0).

ah d'accord, merci beaucoup pour votre aide

[MARJORIE 35390]

ah d'accord, merci beaucoup pour votre aide

je suis obligée de passer par le discriminant pour trouver les racines ?

[ElWaner]

Non la c'est plus simple!

L'équation se réécrit
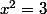
, donc les solutions sont

[MARJORIE 35390]

Non la c'est plus simple!

L'équation se réécrit
, donc les solutions sont et

oooh merci beaucoup beaucoup , c'est trop gentil !!