Bonjour j'ai eu un DM sur les fonctions cubes, mais je n'ai jamais fait d'inequation/equation avec des cubes je suis perdu. Je dois resoudre :
x au cube = 8
2x au cube - 16 = 0
(1+x) au cube = 8
x au cube superieur ou a egale a 64
et -8 inferieur ou egal a x au cube inferieur a 27
Quelqu'un aurait une idée pour me faire comprendre comment on fait s'il vous plait ?
Equation fonction cube
9 messages
- Page 1 sur 1
Re: equation fonction cube
Bonjour,
Il suffit de savoir deux choses :
- La fonction "cube" est strictement croissante sur (il suffit de la dériver pour s'en convaincre)
(il suffit de la dériver pour s'en convaincre)
- Les valeurs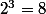 et
et 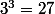 sont à connaître
sont à connaître 
Il suffit de savoir deux choses :
- La fonction "cube" est strictement croissante sur
- Les valeurs
Re: equation fonction cube
Tu n'as pas vu le cours sur les racines nièmes ?
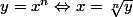
Modifié en dernier par laetidom le 17 Sep 2016, 13:16, modifié 3 fois.
Re: equation fonction cube
Oui mais je ne vois pas comment on peut utiliser ça dans ce cas, non je n'ai pas vu de cours du tout sur le cube 

Re: equation fonction cube
(1+x)^3 = (1+x)²(1+x) = 8
x^3+3x²+3x-7=0 avec solution évidente x=1
on divise par x-1
x^3+3x²+3x-7= (x-1)(x²+4x+7) . . .facile à résoudre . . .
x^3+3x²+3x-7=0 avec solution évidente x=1
on divise par x-1
x^3+3x²+3x-7= (x-1)(x²+4x+7) . . .facile à résoudre . . .
Re: equation fonction cube
Bonjour,
La fonction cube est strictement croissante sur .
.
Pour te donner un exemple, on a alors :
car :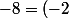^3)
La fonction cube est strictement croissante sur
Pour te donner un exemple, on a alors :
car :
Re: equation fonction cube
laetidom a écrit:Tu n'as pas vu le cours sur les racines nièmes ?
Attention, ceci n'est vrai que pour les entiers n impairs. Pour n=2 par exemple, on a aussi
Re: equation fonction cube
Pseuda a écrit:laetidom a écrit:Tu n'as pas vu le cours sur les racines nièmes ?
Attention, ceci n'est vrai que pour les entiers n impairs. Pour n=2 par exemple, on a aussi
ah oui, merci Pseuda, je viens de vérifier : (x,y) élément de R et n élément de N
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
